
科目: 来源: 题型:
【题目】已知圆![]() :
: ![]() ,直线
,直线![]() 与
与
圆![]() 相切,且直线
相切,且直线![]() :
: ![]() 与椭圆
与椭圆![]() :
: ![]()
相交于![]() 两点,
两点, ![]() 为原点。
为原点。
(1)若直线![]() 过椭圆
过椭圆![]() 的左焦点,且与圆
的左焦点,且与圆![]() 交于
交于![]()
两点,且![]() ,求直线
,求直线![]() 的方程;
的方程;
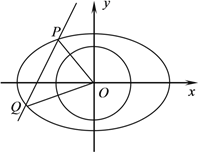
(2)如图,若![]() 的重心恰好在圆上,求
的重心恰好在圆上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义2×2矩阵 ![]() =a1a4﹣a2a3 , 若f(x)=
=a1a4﹣a2a3 , 若f(x)=  ,则f(x)的图象向右平移
,则f(x)的图象向右平移 ![]() 个单位得到函数g(x),则函数g(x)解析式为( )
个单位得到函数g(x),则函数g(x)解析式为( )
A.g(x)=﹣2cos2x
B.g(x)=﹣2sin2x
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系中,以坐标原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点![]() 的极坐标为
的极坐标为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() 为参数).
为参数).
(1)直线![]() 过
过![]() 且与曲线
且与曲线![]() 相切,求直线
相切,求直线![]() 的极坐标方程;
的极坐标方程;
(2)点![]() 与点
与点![]() 关于
关于![]() 轴对称,求曲线
轴对称,求曲线![]() 上的点到点
上的点到点![]() 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】对任意一个确定的二面角α﹣l﹣β,a和b是空间的两条异面直线,在下面给出的四个条件中,能使a和b所成的角也确定的是( )
A.a∥a且b∥β
B.a∥a且b⊥β
C.aα且b⊥β
D.a⊥α且b⊥β
查看答案和解析>>
科目: 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工某零件所花费的时间,为此做了四次实验,得到的数据如表:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程y= ![]() x+
x+ ![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工6个零件需要多少时间?
(注: ![]() =
= 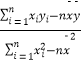 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱锥D﹣ABC中,已知△BCD是正三角形,平面ABC⊥平面BCD,AB=BC=a,AC= ![]() a,E为BC的中点,F在棱AC上,且AF=3FC.
a,E为BC的中点,F在棱AC上,且AF=3FC. 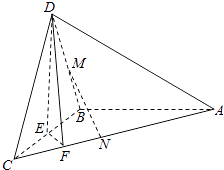
(1)求三棱锥D﹣ABC的体积;
(2)求证:AC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN= ![]() CA,求证:MN∥平面DEF.
CA,求证:MN∥平面DEF.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组: ![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.

(1)求直方图中![]() 的值;
的值;
(2)求续驶里程在![]() 的车辆数;
的车辆数;
(3)若从续驶里程在![]() 的车辆中随机抽取2辆车,求其中恰有一辆车的续驶里程为
的车辆中随机抽取2辆车,求其中恰有一辆车的续驶里程为![]() 的概率.
的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】空气质量主要受污染物排放量及大气扩散等因素的影响,某市环保监测站2014年10月连续10天(从左到右对应1号至10号)采集该市某地平均风速及空气中氧化物的日均浓度数据,制成散点图如图所示.
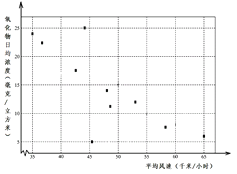
(Ⅰ)同学甲从这10天中随机抽取连续5天的一组数据,计算回归直线方程.试求连续5天的一组数据中恰好同时包含氧化物日均浓度最大与最小值的概率;
(Ⅱ)现有30名学生,每人任取5天数据,对应计算出30个不同的回归直线方程.已知30组数据中有包含氧化物日均浓度最值的有14组.现采用这30个回归方程对某一天平均风速下的氧化物日均浓度进行预测,若预测值与实测值差的绝对值小于2,则称之为“拟合效果好”,否则为“拟合效果不好”.根据以上信息完成下列2×2联表,并分析是否有95%以上的把握说拟合效果与选取数据是否包含氧化物日均浓度最值有关.
预测效果好 | 拟合效果不好 | 合计 | |
数据有包含最值 | 5 | ||
数据无包含最值 | 4 | ||
合计 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
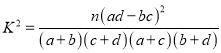 (其中
(其中![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com