[题目]已知椭圆:+=1.左右焦点分别为F1 . F2 . 过F1的直线l交椭圆于A.B两点.若AF2+BF2的最大值为5.则椭圆方程为题目和参考答案——青夏教育精英家教网—

【题目】已知椭圆：+=1，左右焦点分别为F1 ， F2 ，过F1的直线l交椭圆于A，B两点，若AF2+BF2的最大值为5，则椭圆方程为

【答案】
【解析】解：|AF2|+|BF2|=4a﹣|AB|=8﹣|AB|，
∵|AF2|+|BF2|的最大值为5，
∴|AB|的最小值为3．
由题意可设直线l的方程为：my=x+c，（直线l的斜率为0不必考虑），A（x1 ， y1），B（x2 ， y2）．
联立，化为：（b2m2+4）y2﹣2mcb2y+b2c2﹣4b2=0，c2=4﹣b2 ．
∴y1+y2=
∴|AB|==
当m=0时，|AB|=b2；
当m≠0时，|AB|=4+＞b2 ．
∴b2=3．
∴椭圆的标准方程为：，
所以答案是：．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】函数f（x）=ax2﹣2ax+b（a≠0）在闭区间[1，2]上有最大值0，最小值﹣1，则a，b的值为（）
A.a=1，b=0
B.a=﹣1，b=﹣1
C.a=1，b=0或a=﹣1，b=﹣1
D.以上答案均不正确

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在五面体ABCDEF中，FA⊥平面ABCD，AD∥BC∥FE，AB⊥AD，M为EC的中点，AF=AB=BC=FE= AD，

（1）求异面直线BF与DE所成的角的大小；
（2）证明平面AMD⊥平面CDE；
（3）求二面角A﹣CD﹣E的余弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某工科院校对，两个专业的男女生人数进行调查，得到如下的列联表：

	专业	专业	总计
女生	12	4	16
男生	38	46	84
总计	50	50	100

（Ⅰ）从专业的女生中随机抽取2名女生参加某项活动，其中女生甲被选到的概率是多少？

（Ⅱ）能否有95%的把握认为工科院校中“性别”与“专业”有关系？

附：．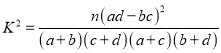

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程（单次充电后能行驶的最大里程），被调查汽车的续驶里程全部介于50公里和300公里之间，将统计结果分成5组：，绘制成如图所示的频率分布直方图.

（1）求直方图中的值；

（2）求续驶里程在的车辆数；

（3）若从续驶里程在的车辆中随机抽取2辆车，求其中恰有一辆车的续驶里程为的概率.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图（示意），公路AM、AN围成的是一块顶角为α的角形耕地，其中tanα＝－2．在该块土地中P处有一小型建筑，经测量，它到公路AM，AN的距离分别为3km，km．现要过点P修建一条直线公路BC，将三条公路围成的区域ABC建成一个工业园．为尽量减少耕地占用，问如何确定B点的位置，使得该工业园区的面积最小？并求最小面积．

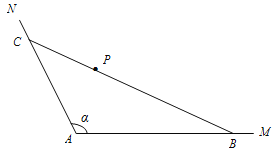
查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=x3+ax2+bx+a2（a＞0）在x=1处有极值10．
（1）求a、b的值；
（2）求f（x）的单调区间；
（3）求f（x）在[0，4]上的最大值与最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】正方体ABCD﹣A1B1C1D1中，E、F分别是AA1、AB的中点，则EF与对角面A1C1CA所成角的度数是（）
A.30°
B.45°
C.60°
D.150°

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】高三年级从甲（文）、乙（理）两个科组各选出7名学生参加高校自主招生数学选拔考试，他们取得的成绩的茎叶图如图所示，其中甲组学生的平均分是85，乙组学生成绩的中位数是83．

（1）求x和y的值；
（2）计算甲组7位学生成绩的方差S2 ．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学