【题目】在平面直角坐标系xOy中，已知曲线C1的参数方程为 （φ为参数）．以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=4 cosθ．
（1）求C1与C2交点的直角坐标；
（2）已知曲线C3的参数方程为 （0≤α＜π，t为参数，且t≠0），C3与C1相交于点P，C2与C3相交于点Q，且|PQ|=8，求α的值．

【题目】秦九韶是我国南宋时期的数学家，他所著的《九章算术》是我国古代数学名著，体现了我国古代数学的辉煌成就．其中的“更相减损术”蕴含了丰富的思想，根据“更相减损术”的思想设计了如图所示的程序框图，若输入的a=15，输出的a=3，则输入的b可能的值为（ ）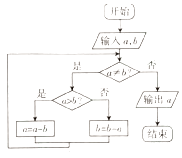
A.30
B.18
C.5
D.4

【题目】已知函数.

（1）当时，求曲线在点处的切线方程；

（2）若有两个零点，求的取值范围.

【题目】（本小题满分12分）设函数.

(Ⅰ)讨论函数的单调性；

(Ⅱ)当函数有最大值且最大值大于时，求的取值范围.

【题目】已知函数f（x）=﹣ x2+（a﹣1）x+lnx．
（1）若a＞﹣1，求函数f（x）的单调区间；
（2）若g（x）= x2+（1﹣2a）x+f（x）有且只有两个零点，求实数a的取值范围．

【题目】甲、乙两人的各科成绩如茎叶图所示，则下列说法正确的是（ ）
A.甲的中位数是89，乙的中位数是98
B.甲的各科成绩比乙各科成绩稳定
C.甲的众数是89，乙的众数是98
D.甲、乙二人的各科成绩的平均分不相同

【题目】已知A（x1 ， f（x1），B（x2 ， f（x2））是函数f（x）=2sin（ωx+φ）（ω＞0，﹣ ＜φ＜0）图象上的任意两点，且初相φ的终边经过点P（1，﹣ ），若|f（x1）﹣f（x2）|=4时，|x1﹣x2|的最小值为 ． （Ⅰ）求函数f（x）的解析式；
（Ⅱ）当x∈[0， ]时，求函数f（x）的单调递增区间；
（Ⅲ）当x∈[0， ]时，不等式mf（x）+2m≥f（x）恒成立，求实数m的取值范围．

【题目】如图，扇形OAB的半径为1，圆心角为120°，四边形PQRS是扇形的内接矩形，当其面积最大时，求点P的位置，并求此最大面积．

【题目】某同学用“五点法”画函数f（x）=Asin（ωx+φ） 在某一个周期内的图象时，列表并填入了部分数据，如表：

（1）请将如表数据补充完整，并直接写出函数f（x）的解析式；
（2）将函数y=f（x）的图象向左平移 个单位长度，得到函数y=g（x）的图象，求y=g（x）的图象离原点O最近的对称中心．
（3）求当 时，函数y=g（x）的值域．

【题目】已知函数f（x）=1+2sinxcosx+2cos2x．
（1）求f（x）递增区间；
（2）求f（x）的对称轴方程；
（3）求f（x）的最大值并写出取最大值时自变量x的集合．