
科目: 来源: 题型:
【题目】某蛋糕店出售一种蛋糕,这种蛋糕的保质期很短,必须当天卖掉,否则容易变质,该蛋糕店每天以每块16元的成本价格制作这种蛋糕若干块,然后以每块26元的价格出售,如果当天卖不完,剩下的蛋糕只能以每块6元低价出售.蛋糕店记录了100天该种蛋糕的日需求量n(单位:块,n∈N*)整理得如图: 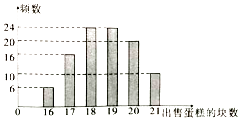
(1)若该蛋糕店某一天制作19块蛋糕,求当天的利润y(单位:元)关于当天需求量n的函数解析式;
(2)若要求出售“出售的蛋糕块数不小于n”的频率不小于0.4,求n的最大值.
(3)若该蛋糕店这100天每天都制作19块蛋糕,试计算这100天蛋糕店所获利润的平均数.
查看答案和解析>>
科目: 来源: 题型:
【题目】假设小明家订了一份报纸,送报人可能在早上6:30﹣7:30之间把报纸送到小明家,小明父亲离开家去工作的时间在早上7:00﹣8:00之间,问小明父亲在离开家前能得到报纸(称为事件A)的概率是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】抽样调查某大型机器设备使用年限x和该年支出维修费用y(万元),得到数据如表
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
部分数据分析如下 ![]() =25,
=25, ![]() yi=112.3,
yi=112.3, ![]() =90
=90
参考公式:线性回归直线方程为 ![]() ,
, 
(1)求线性回归方程;
(2)由(1)中结论预测第10年所支出的维修费用.
查看答案和解析>>
科目: 来源: 题型:
【题目】袋中共有15个除了颜色外完全相同的球,其中有10个白球,5个红球.从袋中任取2个球,所取的2个球中恰有1个白球,1个红球的概率为( )
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆![]() 上异于长轴端点的两点.
上异于长轴端点的两点.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() :
: ![]() ,且
,且![]() ,垂足为
,垂足为![]() ,
, ![]() ,垂足为
,垂足为![]() ,若
,若![]() ,且
,且![]() 的面积是
的面积是![]() 面积的5倍,求
面积的5倍,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为 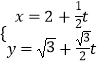 (t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρ=2.
(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρ=2.
(1)若点M的直角坐标为(2, ![]() ),直线l与曲线C1交于A、B两点,求|MA|+|MB|的值.
),直线l与曲线C1交于A、B两点,求|MA|+|MB|的值.
(2)设曲线C1经过伸缩变换 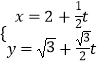 得到曲线C2 , 求曲线C2的内接矩形周长的最大值.
得到曲线C2 , 求曲线C2的内接矩形周长的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,已知曲线C1的参数方程为 ![]() (φ为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4
(φ为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4 ![]() cosθ.
cosθ.
(1)求C1与C2交点的直角坐标;
(2)已知曲线C3的参数方程为 ![]() (0≤α<π,t为参数,且t≠0),C3与C1相交于点P,C2与C3相交于点Q,且|PQ|=8,求α的值.
(0≤α<π,t为参数,且t≠0),C3与C1相交于点P,C2与C3相交于点Q,且|PQ|=8,求α的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com