
科目: 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,AB∥CD,∠BAD=90°,AD= ![]() ,DC=2AB=2,E为BC中点.
,DC=2AB=2,E为BC中点. 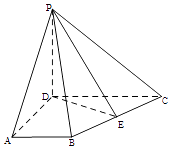
(1)求证:平面PBC⊥平面PDE
(2)线段PC上是否存在一点F,使PA∥平面BDF?若存在,求 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 设an是Sn与2的等差中项,数列{bn}中,b1=1,点P(bn , bn+1)在直线y=x+2上.
(1)求an , bn;
(2)若数列{bn}的前n项和为Bn , 比较 ![]() +
+ ![]() +…+
+…+ ![]() 与1的大小.
与1的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】上面图给出的是计算1+2+4+…+22017的值的一个程序框图,则其中判断框内应填入的是( ) 
A.i=2017?
B.i≥2017?
C.i≥2018?
D.i≤2018?
查看答案和解析>>
科目: 来源: 题型:
【题目】△ABC中内角A,B,C的对边分别为a,b,c,向量 ![]() =(2sinB,﹣
=(2sinB,﹣ ![]() ),
), ![]() =(cos2B,2cos2
=(cos2B,2cos2 ![]() ﹣1)且
﹣1)且 ![]() ∥
∥ ![]() .
.
(1)求锐角B的大小;
(2)如果b=2,求△ABC的面积S△ABC的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】ABCD为空间四边形,AB=CD,AD=BC,AB≠AD,M,N分别是对角线AC与BD的中点,则MN与( )
A.AC,BD之一垂直
B.AC,BD都垂直
C.AC,BD都不垂直
D.AC,BD不一定垂直
查看答案和解析>>
科目: 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn , 且2Sn=(an﹣1)(an+2),
(1)求数列{an}的通项公式
(2)设数列{ ![]() }的前n项和为Tn , 试比较Tn与
}的前n项和为Tn , 试比较Tn与 ![]() 的大小.
的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC 中,角A,B,C所对的边分別为a,b,c,且asin Acos C+csin AcosA= ![]() c
c
(1)若c=1,sin C= ![]() ,求△ABC的面积S
,求△ABC的面积S
(2)若D 是AC的中点且cosB= ![]() ,BD=
,BD= ![]() ,求△ABC的最短边的边长.
,求△ABC的最短边的边长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在三棱锥P﹣ABC中,PA⊥平面ABC,AB=BC=AC=2,PA= ![]() ,E,F分别是PB,BC的中点,则EF与平面PAB所成的角等于( )
,E,F分别是PB,BC的中点,则EF与平面PAB所成的角等于( )
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目: 来源: 题型:
【题目】已知Sn为等比数列{an}的前n项和且S4=S3+3a3 , a2=9.
(1)求数列{an}的通项公式
(2)设bn=(2n﹣1)an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com