（Ⅰ）写出价格f（x）关于时间x的函数关系式（x表示投放市场的第x天，x∈N*）；
（Ⅱ）销售量g（x）与时间x的函数关系式为 ，则该产品投放市场第几天的销售额最高？最高为多少千元？

【题目】已知向量 =（{cosx，﹣ cosx）， =（cosx，sinx），函数f（x）= +1． （Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）若f（θ）= ， 的值．

【题目】已知等差数列{an}的前n项和Sn ， 且a3=7，S11=143， （Ⅰ）求数列{an}的通项公式；
（Ⅱ）设bn=2 +2n，求数列{bn}的前n项和Tn ．

【题目】公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形面积可无限逼近于圆的面积，并创立了“割圆术”，利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14，这就是著名的“徽率”．如图是利用刘徽的“割圆术”思想设计的一个程序框图，则输出的（四舍五入精确到小数点后两位）的值为（ ）（参考数据：sin15°=0.2588，sin75°=0.1305）
A.3.10
B.3.11
C.3.12
D.3.13

【题目】已知函数f（x）=ax﹣lnx（a∈R）．
（1）当a=1时，求f（x）的最小值；
（2）若存在x∈[1，3]，使 +lnx=2成立，求a的取值范围；
（3）若对任意的x∈[1，+∞），有f（x）≥f（ ）成立，求a的取值范围．

【题目】在平面直角坐标系xOy中，椭圆E： =1（a＞b＞0）的离心率为 ，两个顶点分别为A（﹣a，0），B（a，0），点M（﹣1，0），且3 = ，过点M斜率为k（k≠0）的直线交椭圆E于C，D两点，其中点C在x轴上方．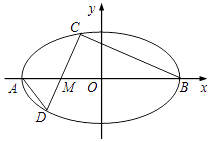
（1）求椭圆E的方程；
（2）若BC⊥CD，求k的值；
（3）记直线AD，BC的斜率分别为k1 ， k2 ， 求证： 为定值．

【题目】某休闲广场中央有一个半径为1（百米）的圆形花坛，现计划在该花坛内建造一条六边形观光步道，围出一个由两个全等的等腰梯形（梯形ABCF和梯形DEFC）构成的六边形ABCDEF区域，其中A、B、C、D、E、F都在圆周上，CF为圆的直径（如图）．设∠AOF=θ，其中O为圆心．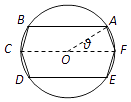
（1）把六边形ABCDEF的面积表示成关于θ的函数f（θ）；
（2）当θ为何值时，可使得六边形区域面积达到最大？并求最大面积．

【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，若acosA=bsinb，且 ，则sinA+sinC的最大值是 ．

【题目】在平面直角坐标系xOy中，已知圆M的圆心在直线y=﹣2x上，且圆M与直线x+y﹣1=0相切于点P（2，﹣1）．
（1）求圆M的方程；
（2）过坐标原点O的直线l被圆M截得的弦长为 ，求直线l的方程．