
科目: 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)+B,A>0,ω>0,|φ|< ![]() 在某一个周期的图象时,列表并填入了部分数据,如表:
在某一个周期的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x | x1 |
| x2 |
| x3 |
Asin(ωx+φ)+B | 0 |
| 0 | ﹣ | 0 |
(1)请求出上表中的x1 , x2 , x3 , 并直接写出函数f(x)的解析式;
(2)若3sin2 ![]() ﹣
﹣ ![]() mf(
mf( ![]() ﹣
﹣ ![]() )≥m+2对任意x∈[0,2π]恒成立,求实数m的取值范围.
)≥m+2对任意x∈[0,2π]恒成立,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线y=x2﹣6x+1与坐标轴的交点都在圆C上.
(Ⅰ)求圆C的方程;
(Ⅱ)若圆C与直线x﹣y+a=0交与A,B两点,且OA⊥OB,求a的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设a∈R,函数f(x)=cosx(asinx﹣cosx)+cos2( ![]() ﹣x)满足f(﹣
﹣x)满足f(﹣ ![]() )=f(0).
)=f(0).
(1)求f(x)的单调递减区间;
(2)设锐角△ABC的内角A,B,C所对的边分别为a,b,c,且 ![]() =
= ![]() ,求f(A)的取值范围.
,求f(A)的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP= ![]() .
.
(Ⅰ)求证:AB⊥PC;
(Ⅱ)求点D到平面PAC的距离.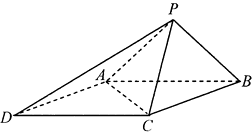
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}满足an+1=λan+2n(n∈N* , λ∈R),且a1=2.
(1)若λ=1,求数列{an}的通项公式;
(2)若λ=2,证明数列{ ![]() }是等差数列,并求数列{an}的前n项和Sn .
}是等差数列,并求数列{an}的前n项和Sn .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在正三棱柱ABC﹣A1B1C1中,点D在边BC上,AD⊥C1D. 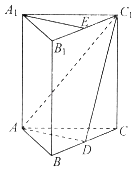
(1)求证:平面ADC1⊥平面BCC1B1;
(2)如果点E是B1C1的中点,求证:AE∥平面ADC1 .
查看答案和解析>>
科目: 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(Ⅰ)求C;
(Ⅱ)若c= ![]() ,△ABC的面积为
,△ABC的面积为 ![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面上的三个向量,其中
是同一平面上的三个向量,其中 ![]() =(1,2).
=(1,2).
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标.
的坐标.
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 垂直,求
垂直,求 ![]() 与
与 ![]() 的夹角θ
的夹角θ
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com