
【题目】设△ABC的内角A,B,C的对边分别为a,b,c,且bcosA= ![]() asinB.
asinB.
(1)求角A的大小;
(2)若a=1,求△ABC面积的最大值.
【答案】
(1)解:在△ABC中,∵ ![]() asinB=bcosA.
asinB=bcosA.
由正弦定理,得: ![]() sinAsinB=sinBcosA,
sinAsinB=sinBcosA,
∵0<B<π,sinB≠0.
∴ ![]() sinA=cosA,即tanA=
sinA=cosA,即tanA= ![]() .
.
∵0<A<π,
∴A= ![]() .
.
(2)解:∵由a=1,A= ![]() ,
,
∴由余弦定理,1=b2+c2﹣ ![]() bc≥2bc﹣
bc≥2bc﹣ ![]() bc,得:bc≤2
bc,得:bc≤2 ![]() ,当且仅当b=c等号成立,
,当且仅当b=c等号成立,
∴△ABC的面积S= ![]() bcsinA≤
bcsinA≤ ![]() (2+
(2+ ![]() )×
)× ![]() =
= ![]() ,即△ABC面积的最大值为
,即△ABC面积的最大值为 ![]() .
.
【解析】(1)根据正弦定理化简可得 ![]() sinAsinB=sinBcosA,结合sinB≠0,可求tanA,由范围0<A<π,可求A的值.(2)由已知利用余弦定理,基本不等式可求bc≤2
sinAsinB=sinBcosA,结合sinB≠0,可求tanA,由范围0<A<π,可求A的值.(2)由已知利用余弦定理,基本不等式可求bc≤2 ![]() ,进而利用三角形面积公式即可计算得解.
,进而利用三角形面积公式即可计算得解.
【考点精析】通过灵活运用正弦定理的定义,掌握正弦定理:![]() 即可以解答此题.
即可以解答此题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】二手车经销商小王对其所经营的某一型号二手汽车的使用年数x(0<x≤10)与销售价格y(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
参考公式: 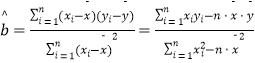 ,
, ![]() .
.
(1)若这两个变量呈线性相关关系,试求y关于x的回归直线方程 ![]() ;
;
(2)已知小王只收购使用年限不超过10年的二手车,且每辆该型号汽车的收购价格为ω=0.03x2﹣1.81x+16.2万元,根据(1)中所求的回归方程,预测x为何值时,小王销售一辆该型号汽车所获得的利润L(x)最大? (销售一辆该型号汽车的利润=销售价格﹣收购价格)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣(a+1)x+b.
(1)若f(x)<0的解集为(﹣1,3),求a,b的值;
(2)当a=1时,若对任意x∈R,f(x)≥0恒成立,求实数b的取值范围;
(3)当b=a时,解关于x的不等式f(x)<0(结果用a表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}前n项和为Sn .
(1)若Sn=2n﹣1,求数列{an}的通项公式;
(2)若a1= ![]() ,Sn=anan+1 , an≠0,求数列{an}的通项公式;
,Sn=anan+1 , an≠0,求数列{an}的通项公式;
(3)设无穷数列{an}是各项都为正数的等差数列,是否存在无穷等比数列{bn},使得an+1=anbn恒成立?若存在,求出所有满足条件的数列{bn}的通项公式;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP= ![]() .
.
(Ⅰ)求证:AB⊥PC;
(Ⅱ)求点D到平面PAC的距离.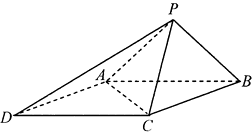
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项为正的等比数列{an}的前n项和为Sn , S4=30,过点P(n,log2an)和Q(n+2,log2an+1)(n∈N*)的直线的一个方向向量为(﹣1,﹣1)
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,数列{bn}的前n项和为Tn , 证明:对于任意n∈N* , 都有Tn
,数列{bn}的前n项和为Tn , 证明:对于任意n∈N* , 都有Tn ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知圆C的方程:x2+y2﹣2x﹣4y+4=0,点P是直线l:x﹣2y﹣2=0上的任意点,过P作圆的两条切线PA,PB,切点为A、B,当∠APB取最大值时.
(Ⅰ)求点P的坐标及过点P的切线方程;
(Ⅱ)在△APB的外接圆上是否存在这样的点Q,使|OQ|= ![]() (O为坐标原点),如果存在,求出Q点的坐标,如果不存在,请说明理由.
(O为坐标原点),如果存在,求出Q点的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知锐角三角形的两个内角A,B满足 ![]() ,则有( )
,则有( )
A.sin2A﹣cosB=0
B.sin2A+cosB=0
C.sin2A+sinB=0
D.sin2A﹣sinB=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com