【题目】如图所示，四棱锥P－ABCD的底面ABCD是边长为1的菱形，∠BCD＝60°，E是CD的中点，PA⊥底面ABCD，PA＝.

(1)证明：平面PBE⊥平面PAB；

(2)求二面角A－BE－P的大小．

【题目】已知直线经过直线与的交点.

(1)点到直线的距离为3，求直线的方程；

(2)求点到直线的距离的最大值,并求距离最大时的直线的方程．

如图，在三棱锥P—ABC中，PC⊥底面ABC，AB⊥BC，D，E分别是AB，PB的中点．

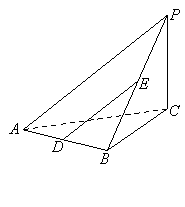
(1)求证：DE∥平面PAC

(2)求证：AB⊥PB

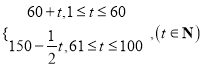【题目】经市场调查,某商品在过去的100天内的销售量(单位:件)和价格(单位:元)均为时间 (单位:天)的函数,且销售量满足=,价格满足=.

(1)求该种商品的日销售额与时间的函数关系;

(2)若销售额超过16610元,商家认为该商品的收益达到理想程度,请判断该商品在哪几天的收益达到理想程度?

A. 平面平面ABCD

B. 直线BE,CF相交于一点

C. EF//平面BGD

D. 平面BGD

【题目】已知函数（，且）．

（1）当时，设集合，求集合；

（2）在（1）的条件下，若，且满足，求实数的取值范围；

（3）若对任意的，存在，使不等式恒成立，求实数的取值范围．

【题目】在（1+x+x2）n= x x2+… xr+… x2n﹣1 x2n的展开式中，把D ，D ，D …，D …，D 叫做三项式系数
（1）求D 的值
（2）根据二项式定理，将等式（1+x）2n=（1+x）n（x+1）n的两边分别展开可得，左右两边xn的系数相等，即C =（C ）2+（C ）2+（C ）2+…+（C ）2 ， 利用上述思想方法，请计算D C ﹣D C +D C ﹣…+（﹣1）rD C +.. C C 的值．

【题目】在校运动会上，甲、乙、丙三位同学每人均从跳远，跳高，铅球，标枪四个项目中随机选一项参加比赛，假设三人选项目时互不影响，且每人选每一个项目时都是等可能的
（1）求仅有两人所选项目相同的概率；
（2）设X为甲、乙、丙三位同学中选跳远项目的人数，求X的分布列和数学期望E（X）

【题目】已知函数f（x）=lnx﹣ （a＞0）
（1）若函数f（x）在x=2处的切线与x轴平行，求实数a的值；
（2）讨论函数f（x）在区间[1，2]上的单调性；
（3）证明： ＞e．