【题目】如图，已知椭圆 =1（a＞b＞0），F1 ， F2分别为椭圆的左、右焦点，A为椭圆的上顶点，直线AF2交椭圆于另一点B．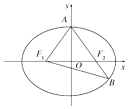

（1）若∠F1AB=90°，求椭圆的离心率；
（2）若椭圆的焦距为2，且 =2 ，求椭圆的方程．

【题目】我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准x（吨），一位居民的月用水量不超过x的部分按平价收费，超出x的部分按议价收费．为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0，0.5），[0.5，1），…，[4，4.5）分成9组，制成了如图所示的频率分布直方图．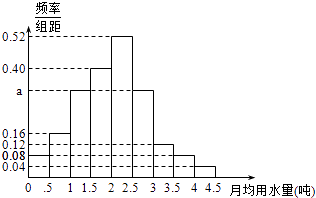

（Ⅰ）求直方图中a的值；
（Ⅱ）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由；
（Ⅲ）若该市政府希望使85%的居民每月的用水量不超过标准x（吨），估计x的值，并说明理由．

【题目】在中，角的对边分别为，且成等差数列

（1）若，求的面积

（2）若成等比数列，试判断的形状

摸球方法：从袋中随机摸出3个球，若摸得同一颜色的3个球，摊主送给摸球者5元钱；若摸得非同一颜色的3个球，摸球者付给摊主1元钱．

（1）摸出的3个球为白球的概率是多少？

（2）摸出的3个球为2个黄球1个白球的概率是多少？

（3）假定一天中有100人次摸奖，试从概率的角度估算一下这个摊主一个月（按30天计）能赚多少钱？

【题目】P（x0 ， y0）（x0≠±a）是双曲线E： 上一点，M，N分别是双曲线E的左右顶点，直线PM，PN的斜率之积为 ．
（1）求双曲线的离心率；
（2）过双曲线E的右焦点且斜率为1的直线交双曲线于A，B两点，O为坐标原点，C为双曲线上一点，满足 ，求λ的值．

【题目】双曲线 =1（a＞1，b＞0）的焦点距为2c，直线l过点（a，0）和（0，b），且点（1，0）到直线l的距离与点（﹣1，0）到直线l的距离之和 ．求双曲线的离心率e的取值范围．

根据以上样本数据，她建立了身高 （cm）与年龄x（周岁）的线性回归方程为 ，给出下列结论：
①y与x具有正的线性相关关系；
②回归直线过样本的中心点（42，117.1）；
③儿子10岁时的身高是 cm；
④儿子年龄增加1周岁，身高约增加 cm.
其中，正确结论的个数是
A.1
B.2
C.3
D.4

【题目】F1、F2为椭圆的两个焦点，以F2为圆心作圆F2 ， 已知圆F2经过椭圆的中心，且与椭圆相交于M点，若直线MF1恰与圆F2相切，则该椭圆的离心率e为（　　）
A. ﹣1
B.2﹣
C.
D.

(1)若α＝75°，R＝12 cm，求扇形的弧长l和面积；

(2)若扇形的周长为20 cm，当扇形的圆心角α为多少弧度时，这个扇形的面积最大？