【题目】我市“金牛”公园欲在长、宽分别为 、的矩形地块内开凿一“挞圆”形水池（如图），池边由两个半椭圆和（）组成，其中，“挞圆”内切于矩形且其左右顶点， 和上顶点构成一个直角三角形．

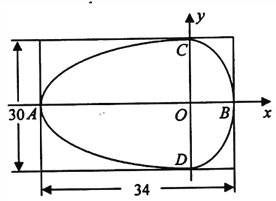
（1）试求“挞圆”方程；

（2）若在“挞圆”形水池内建一矩形网箱养殖观赏鱼，则该网箱水面面积最大为多少？

【题目】如图，在正四棱柱中， ， ，点是的中点，点在上．　

（1）若异面直线和所成的角为，求的长；

（2）若，求二面角的余弦值．

【题目】已知点是圆：上任意一点，点与点关于原点对称，线段的垂直平分线与交于点.

（1）求点的轨迹的方程；

（2）过点的动直线与点的轨迹交于两点，在轴上是否存在定点使以为直径的圆恒过这个点？若存在，求出点的坐标；若不存在，请说明理由.

【题目】如图，已知圆的半径为，,是圆上的一个动点，的中垂线交于点，以直线为轴，的中垂线为轴建立平面直角坐标系。

（Ⅰ）若点的轨迹为曲线，求曲线的方程；

（Ⅱ）设点为圆上任意一点，过作圆的切线与曲线交于两点，证明：以为直径的圆经过定点，并求出该定点的坐标。

【题目】如图，四棱锥中，底面为平行四边形， ， ， 底面.

（1）证明：平面平面；

（2）若二面角的大小为，求与平面所成角的正弦值.

【题目】已知数列{an}的前n项和为Sn ， 且对任意正整数n，都有an= +2成立．
（1）记bn=log2an ， 求数列{bn}的通项公式；
（2）设cn= ，求数列{cn}的前n项和Tn ．

（1）设使用年该车的总费用（包括购车费用）为，试写出的表达式；

（2）问这种新能源汽车使用多少年报废最合算（即该车使用多少年平均费用最少），年平均费用的最小值是多少？

【题目】已知函数是定义域为的奇函数，当.

（Ⅰ）求出函数在上的解析式；

（Ⅱ）在答题卷上画出函数的图象，并根据图象写出的单调区间；

（Ⅲ）若关于的方程有三个不同的解，求的取值范围。

①设是两个定点， 为非零常数，若，则动点的轨迹为双曲线的一支；②过定圆上一定点作圆的动弦， 为坐标原点，若，则动点的轨迹为椭圆；③方程的两根可分别作为椭圆和双曲线的离心率；④双曲线与椭圆有相同的焦点.

其中真命题的序号是_______.