练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】2017年12月4日0时起郑州市实施机动车单双号限行，新能源汽车不在限行范围内，某人为了出行方便，准备购买某能源汽车.假设购车费用为14.4万元，每年应交付保险费、充电费等其他费用共0.9万元，汽车的保养维修费为：第一年0.2万元，第二年0.4万元，第三年0.6万元，…，依等差数列逐年递增.

    （1）设使用年该车的总费用（包括购车费用）为，试写出的表达式；

    （2）问这种新能源汽车使用多少年报废最合算（即该车使用多少年平均费用最少），年平均费用的最小值是多少？

    【答案】(1) (2) 这种新能源汽车使用12年报废最合算，年平均费用的最小值是3.4万元.

    【解析】试题分析：（I）由已知中某种汽车购买时费用为14.4万元，每年应交付保险费、养路费及汽油费共0.9万元，汽车的维修费为：第一年0.2万元，第二年0.4万元，第三年0.6万元，…，依等差数列逐年递增，根据等差数列前n项和公式，即可得到f（n）的表达式；

    （II）由（I）中使用n年该车的总费用，我们可以得到n年平均费用表达式，根据基本不等式，我们易计算出平均费用最小时的n值，进而得到结论．

    试题解析：

    解：（1）由题意得

    ，

    （2）设该车的年平均费用为万元，则有

    ，

    当且仅当，即时，等号成立，即取最小值3.4万元.

    答：这种新能源汽车使用12年报废最合算，年平均费用的最小值是3.4万元.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，椭圆C： + =1（a＞b＞0）的离心率是 ，且过点（ ， ）．设点A1 ， B1分别是椭圆的右顶点和上顶点，如图所示过 点A1 ， B1引椭圆C的两条弦A1E、B1F．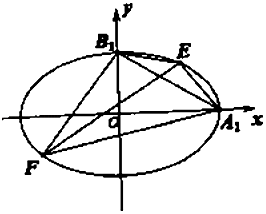

    （1）求椭圆C的方程；
    （2）若直线A1E与B1F的斜率是互为相反数．
    ①求直线EF的斜率k0②设直线EF的方程为y=k0x+b（﹣1≤b≤1）设△A1EF、△B1EF的面积分别为S1和S2 ， 求S1+S2的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）是R上的偶函数，在（﹣3，﹣2）上为减函数且对x∈R都有f（2﹣x）=f（x），若A，B是钝角三角形ABC的两个锐角，则（ ）
    A.f（sinA）＜f（cosB）
    B.f（sinA）＞f（cosB）
    C.f（sinA）=f（cosB）
    D.f（sinA）与与f（cosB）的大小关系不确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某个体经营者把开始六个月试销A、B两种商品的逐月投资与所获纯利润列成下表：

    投资A商品金额（万元）

    1

    2

    3

    4

    5

    6

    获纯利润（万元）

    0.65

    1.39

    1.85

    2

    1.84

    1.40

    投资B商品金额（万元）

    1

    2

    3

    4

    5

    6

    获纯利润（万元）

    0.25

    0.49

    0.76

    1

    1.26

    1.51

    该经营者准备下月投入12万元经营这两种产品，但不知投入A、B两种商品各多少才最合算．请你帮助制定一下资金投入方案，使得该经营者能获得最大利润，并按你的方案求出该经营者下月可获得的最大利润（结果保留两个有效数字）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C的对边分别为a，b，c，且满足条件b2+c2﹣a2=bc=1，cosBcosC=﹣ ，则△ABC的周长为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点是圆：上任意一点，点与点关于原点对称，线段的垂直平分线与交于点.

    （1）求点的轨迹的方程；

    （2）过点的动直线与点的轨迹交于两点，在轴上是否存在定点使以为直径的圆恒过这个点？若存在，求出点的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A＝{x|x2－2x－3≤0}，B＝{x|x2－2mx＋m2－4≤0，x∈R，m∈R}．

    (1)若A∩B＝[0,3]，求实数m的值；

    (2)若ARB，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆E的极坐标方程为ρ=4sinθ，以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，取相同单位长度（其中（ρ，θ），ρ≥0，θ∈[0，2π）））．
    （1）直线l过原点，且它的倾斜角α= ，求l与圆E的交点A的极坐标（点A不是坐标原点）；
    （2）直线m过线段OA中点M，且直线m交圆E于B、C两点，求||MB|﹣|MC||的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，沿河有A、B两城镇，它们相距20千米，以前，两城镇的污水直接排入河里，现为保护环境，污水需经处理才能排放，两城镇可以单独建污水处理厂，或者联合建污 水处理厂（在两城镇之间或其中一城镇建厂，用管道将污水从各城镇向污水处理厂输送），依据经验公式，建厂的费用为f（m）=25m0.7（万元），m表示污水流量，铺设管道的费用（包括管道费） （万元），x表示输送污水管道的长度（千米）；
    已知城镇A和城镇B的污水流量分别为m1=3、m2=5，A、B两城镇连接污水处理厂的管道总长为20千米；假定：经管道运输的污水流量不发生改变，污水经处理后直接排入河中；请解答下列问题（结果精确到0.1）

    （1）若在城镇A和城镇B单独建厂，共需多少总费用？
    （2）考虑联合建厂可能节约总投资，设城镇A到拟建厂的距离为x千米，求联合建厂的总费用y与x的函数关系 式，并求y的取值范围．

    查看答案和解析>>

    同步练习册答案