
【题目】某个体经营者把开始六个月试销A、B两种商品的逐月投资与所获纯利润列成下表:
投资A商品金额(万元) | 1 | 2 | 3 | 4 | 5 | 6 |
获纯利润(万元) | 0.65 | 1.39 | 1.85 | 2 | 1.84 | 1.40 |
投资B商品金额(万元) | 1 | 2 | 3 | 4 | 5 | 6 |
获纯利润(万元) | 0.25 | 0.49 | 0.76 | 1 | 1.26 | 1.51 |
该经营者准备下月投入12万元经营这两种产品,但不知投入A、B两种商品各多少才最合算.请你帮助制定一下资金投入方案,使得该经营者能获得最大利润,并按你的方案求出该经营者下月可获得的最大利润(结果保留两个有效数字).
【答案】分别投资A、B两种商品3.2万元和8.8万元,可获最大利润4.1万元
【解析】
根据表格数据,画出散点图,从而求出函数模型,再设第7个月投入A,B两种商品的资金分别为x万元,总利润为![]() 万元,求出利润函数,利用配方法,即可得到结论.
万元,求出利润函数,利用配方法,即可得到结论.
以投资额为横坐标,纯利润为纵坐标,在直角坐标系中画出散点图(如下图).

据此,可考虑用下列函数分别描述上述两组数据之间的对应关系:
![]() ①
① ![]() ②
②
把![]() ,
,![]() 代入①式,得
代入①式,得![]() ,解得
,解得![]()
故前六个月所获纯利润关于月投资于A种商品的金额的函数关系式可近似的用
![]() 表示
表示
再把![]() ,
,![]() 代入②式,得
代入②式,得![]() ,故前六个月所获纯利润关于月投资于
,故前六个月所获纯利润关于月投资于
B种商品的金额的函数关系式可近似的用![]() 表示
表示
设下月投资于A种商品x万元,则投资于B种商品![]() 万元,可获纯利润:
万元,可获纯利润:
![]()
当![]() 时,
时,![]()
故下月分别投资A、B两种商品3.2万元和8.8万元,可获最大利润4.1万元


科目:高中数学 来源: 题型:
【题目】共享单车的推广给消费者带来全新消费体验,迅速赢得广大消费者的青睐,然而,同时也暴露出管理、停放、服务等方面的问题,为了了解公众对共享单车的态度(提倡或不提倡),某调查小组随机地对不同年龄段50人进行调查,将调查情况整理如下表:

并且,年龄在![]() 和
和![]() 的人中持“提倡”态度的人数分别为5和3,现从这两个年龄段中随机抽取2人征求意见.
的人中持“提倡”态度的人数分别为5和3,现从这两个年龄段中随机抽取2人征求意见.
(Ⅰ)求年龄在![]() 中被抽到的2人都持“提倡”态度的概率;
中被抽到的2人都持“提倡”态度的概率;
(Ⅱ)求年龄在![]() 中被抽到的2人至少1人持“提倡”态度的概率.
中被抽到的2人至少1人持“提倡”态度的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了普及环保知识增强环保意识,某校从理工类专业甲班抽取60人,从文史类乙班抽取50人参加环保知识测试 附:k2= ![]() ,n=a+b+c+d
,n=a+b+c+d
P(K2>k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(1)根据题目条件完成下面2×2列联表,并据此判断你是否有99%的把握认为环保知识与专业有关
优秀 | 非优秀 | 总计 | |
甲班 | |||
乙班 | 30 | ||
总计 | 60 |
(2)为参加上级举办的环保知识竞赛,学校举办预选赛,预选赛答卷满分100分,优秀的同学得60分以上通过预选,非优秀的同学得80分以上通过预选,若每位同学得60分以上的概率为 ![]() ,得80分以上的概率为
,得80分以上的概率为 ![]() ,现已知甲班有3人参加预选赛,其中1人为优秀学生,若随机变量X表示甲班通过预选的人数,求X的分布列及期望E(X).
,现已知甲班有3人参加预选赛,其中1人为优秀学生,若随机变量X表示甲班通过预选的人数,求X的分布列及期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ax﹣lnx,a∈R.
(1)若函数f(x)在[1,2]上是减函数,求实数a的取值范围;
(2)令g(x)=f(x)﹣x2 , 是否存在实数a,当x∈(0,e](e是自然常数)时,函数g(x)的最小值是3,若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年12月4日0时起郑州市实施机动车单双号限行,新能源汽车不在限行范围内,某人为了出行方便,准备购买某能源汽车.假设购车费用为14.4万元,每年应交付保险费、充电费等其他费用共0.9万元,汽车的保养维修费为:第一年0.2万元,第二年0.4万元,第三年0.6万元,…,依等差数列逐年递增.
(1)设使用![]() 年该车的总费用(包括购车费用)为
年该车的总费用(包括购车费用)为![]() ,试写出
,试写出![]() 的表达式;
的表达式;
(2)问这种新能源汽车使用多少年报废最合算(即该车使用多少年平均费用最少),年平均费用的最小值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,平行于
,平行于![]() 轴的两条直线
轴的两条直线![]() 分别交
分别交![]() 于
于![]() 两点,交
两点,交![]() 的准线于
的准线于![]() 两点.
两点.
(1)若![]() 在线段
在线段![]() 上,
上, ![]() 是
是![]() 的中点,证明:
的中点,证明: ![]() ;
;
(2)若![]() 的面积是
的面积是![]() 的面积的两倍,求
的面积的两倍,求![]() 中点的轨迹方程.
中点的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产A,B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图①;B产品的利润与投资的算术平方根成正比,其关系如图②.(注:利润和投资单位:万元)
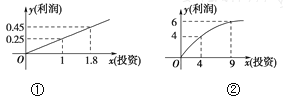
(1)分别将A,B两种产品的利润表示为投资的函数关系式;
(2)已知该企业已筹集到18万元资金,并将全部投入A,B两种产品的生产,怎样分配这18万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com