【题目】已知公差不为零的等差数列{an}中， S2＝16，且成等比数列.

（1）求数列{an}的通项公式；

（2）求数列{|an|}的前n项和Tn.

【题目】如图，己知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E、F分别是AC、AD上的动点，且 =λ（0＜λ＜1）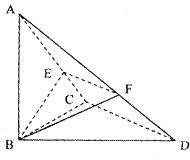
（1）求证：不论λ为何值，总有EF⊥平面ABC：
（2）若λ= ，求三棱锥A﹣BEF的体积．

【题目】一支车队有辆车，某天依次出发执行运输任务。第一辆车于下午时出发，第二辆车于下午时分出发，第三辆车于下午时分出发，以此类推。假设所有的司机都连续开车，并都在下午时停下来休息.

到下午时，最后一辆车行驶了多长时间？

如果每辆车的行驶速度都是,这个车队当天一共行驶了多少?

（1）如果对有线性相关关系，求回归方程；

（2）若实际生产中，允许每小时生产的产品中有缺点的零件最多有1个，那么机器的运转速度应控制在什么范围内？参考公式：， ．

【题目】数列{an}的前n项和记为Sn ， a1=t，an+1=2Sn+1（n∈N*）．
（1）当t为何值时，数列{an}为等比数列？
（2）在（1）的条件下，若等差数列{bn}的前n项和Tn有最大值，且T3=15，又a1+b1 ， a2+b2 ， a3+b3成等比数列，求Tn ．

【题目】在外接圆直径为1的△ABC中，角A，B，C的对边分别为a，b，c，设向量 =（a，cosB）， =（b，cosA），且 ∥ ， ≠ ．
（1）求sinA+sinB的取值范围；
（2）若abx=a+b，试确定实数x的取值范围．

【题目】已知函f（x）=ax2﹣ex（a∈R）． （Ⅰ）a=1时，试判断f（x）的单调性并给予证明；
（Ⅱ）若f（x）有两个极值点x1 ， x2（x1＜x2）．
（i） 求实数a的取值范围；
（ii）证明：﹣ ． （注：e是自然对数的底数）

【题目】已知椭圆C： =1的左焦点F1的坐标为（﹣ ，0），F2是它的右焦点，点M是椭圆C上一点，△MF1F2的周长等于4+2 ．
（1）求椭圆C的方程；
（2）过定点P（0，2）作直线l与椭圆C交于不同的两点A，B，且OA⊥OB（其中O为坐标原点），求直线l的方程．

【题目】三棱锥被平行于底面ABC的平面所截得的几何体如图所示，截面为A1B1C1 ， ∠BAC=90°，A1A⊥平面ABC，A1A= ，AB= ，AC=2，A1C1=1， = ． （Ⅰ）证明：BC⊥平面A1AD
（Ⅱ）求二面角A﹣CC1﹣B的余弦值．

（附：回归直线的斜率和截距的最小二乘法估计公式分别为:，）

（1）求身高关于年龄的线性回归方程；(可能会用到的数据：（cm）)

（2）利用（1）中的线性回归方程，分析张三同学岁起到岁身高的变化情况，如 岁之前都符合这一变化，请预测张三同学 岁时的身高。