【题目】已知函数f0（x）= （x＞0），设fn（x）为fn﹣1（x）的导数，n∈N* ．
（1）求2f1（ ）+ f2（ ）的值；
（2）证明：对任意n∈N* ， 等式|nfn﹣1（ ）+ fn（ ）|= 都成立．

（1）若函数f (x)的图象与函数g(x)的图象相切，求b的值；

（2）设T(x)＝f (x)＋ag(x)，a∈R，求函数T(x)的单调增区间；

（3）设h(x)＝|g(x)|·f (x)，b＜1．若存在x1，x2 [0，1]，使|h(x1)－h(x2)|＞1成立，求b的取值范围．

【题目】盒中共有9个球，其中有4个红球，3个黄球和2个绿球，这些球除颜色外完全相同．
（1）从盒中一次随机取出2个球，求取出的2个球颜色相同的概率P；
（2）从盒中一次随机取出4个球，其中红球、黄球、绿球的个数分别记为x1 ， x2 ， x3 ， 随机变量X表示x1 ， x2 ， x3中的最大数，求X的概率分布和数学期望E（X）．

【题目】设数列{an}的前n项和为Sn ， 若对任意的正整数n，总存在正整数m，使得Sn=am ， 则称{an}是“H数列”．
（1）若数列{an}的前n项和为Sn=2n（n∈N*），证明：{an}是“H数列”；
（2）设{an}是等差数列，其首项a1=1，公差d＜0，若{an}是“H数列”，求d的值；
（3）证明：对任意的等差数列{an}，总存在两个“H数列”{bn}和{cn}，使得an=bn+cn（n∈N*）成立．

（1）求数列{an}的前n项和Sn；

（2）设Tn＝(－1)iai，若对一切正整数n，不等式 λTn＜[an＋1＋(－1)n＋1an]·2n－1 恒成立，求实数 λ 的取值范围；

（3）是否存在正整数m，n(n＞m＞2)，使得S2，Sm－S2，Sn－Sm成等比数列？若存在，求出所有的m，n；若不存在，说明理由．

【题目】已知函数f（x）=ex+e﹣x ， 其中e是自然对数的底数．
（1）证明：f（x）是R上的偶函数；
（2）若关于x的不等式mf（x）≤e﹣x+m﹣1在（0，+∞）上恒成立，求实数m的取值范围；
（3）已知正数a满足：存在x0∈[1，+∞），使得f（x0）＜a（﹣x03+3x0）成立，试比较ea﹣1与ae﹣1的大小，并证明你的结论．

【题目】已知函数，，，令.

（Ⅰ）研究函数的单调性；

（Ⅱ）若关于的不等式恒成立，求整数的最小值；

（Ⅲ），正实数，满足，证明：.

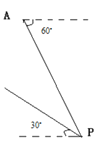
【题目】据监测，在海滨某城市附近的海面有一台风. 台风中心位于城市的东偏南方向、距离城市的海面处，并以的速度向西偏北方向移动（如图示）.如果台风侵袭范围为圆形区域，半径，台风移动的方向与速度不变，那么该城市受台风侵袭的时长为_____ .

【题目】某礼品店要制作一批长方体包装盒，材料是边长为的正方形纸板．如图所示，先在其中相邻两个角处各切去一个边长是的正方形，然后在余下两个角处各切去一个长、宽分别为、的矩形，再将剩余部分沿图中的虚线折起，做成一个有盖的长方体包装盒．

(1)求包装盒的容积关于的函数表达式，并求函数的定义域；

(2)当为多少时，包装盒的容积最大？最大容积是多少？

【题目】如图，为保护河上古桥OA，规划建一座新桥BC，同时设立一个圆形保护区，规划要求：新桥BC与河岸AB垂直；保护区的边界为圆心M在线段OA上并与BC相切的圆，且古桥两端O和A到该圆上任意一点的距离均不少于80m，经测量，点A位于点O正北方向60m处，点C位于点O正东方向170m处（OC为河岸），tan∠BCO= ．

（1）求新桥BC的长；
（2）当OM多长时，圆形保护区的面积最大？