
科目: 来源: 题型:
【题目】某校在本校任选了一个班级,对全班50名学生进行了作业量的调查,根据调查结果统计后,得到如下的![]() 列联表,已知在这50人中随机抽取2人,这2人都“认为作业量大”的概率为
列联表,已知在这50人中随机抽取2人,这2人都“认为作业量大”的概率为![]() .
.
| 认为作业量大 | 认为作业量不大 | 合计 |
男生 | 18 | ||
女生 | 17 | ||
合计 | 50 |
(Ⅰ)请完成上面的列联表;
(Ⅱ)根据列联表的数据,能否有![]() 的把握认为“认为作业量大”与“性别”有关?
的把握认为“认为作业量大”与“性别”有关?
(Ⅲ)若视频率为概率,在全校随机抽取4人,其中“认为作业量大”的人数记为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
附:![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,P为棱C1D1的中点,Q为棱BB1上的点,且BQ=λBB1(λ≠0). 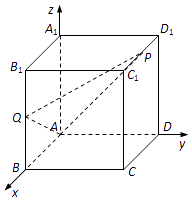
(1)若 ![]() ,求AP与AQ所成角的余弦值;
,求AP与AQ所成角的余弦值;
(2)若直线AA1与平面APQ所成的角为45°,求实数λ的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达
到达![]() 的位置,得到如图所示的四棱锥
的位置,得到如图所示的四棱锥![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
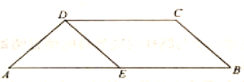
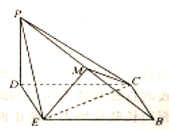
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知等差数列{an}的公差d不为0,且 ![]() ,
, ![]() ,…,
,…, ![]() ,…(k1<k2<…<kn<…)成等比数列,公比为q.
,…(k1<k2<…<kn<…)成等比数列,公比为q.
(1)若k1=1,k2=3,k3=8,求 ![]() 的值;
的值;
(2)当 ![]() 为何值时,数列{kn}为等比数列;
为何值时,数列{kn}为等比数列;
(3)若数列{kn}为等比数列,且对于任意n∈N* , 不等式 ![]() 恒成立,求a1的取值范围.
恒成立,求a1的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】将圆的一组![]() 等分点分别涂上红色或蓝色,从任意一点开始,按逆时针方向依次记录
等分点分别涂上红色或蓝色,从任意一点开始,按逆时针方向依次记录![]() 个点的颜色,称为该圆的一个“
个点的颜色,称为该圆的一个“![]() 阶色序”,当且仅当两个“
阶色序”,当且仅当两个“![]() 阶色序”对应位置上的颜色至少有一个不相同时,称为不同的“
阶色序”对应位置上的颜色至少有一个不相同时,称为不同的“![]() 阶色序”.若某圆的任意两个“
阶色序”.若某圆的任意两个“![]() 阶色序”均不相同,则称该圆为“
阶色序”均不相同,则称该圆为“![]() 阶魅力圆”.“4阶魅力圆”中最多可有的等分点个数为__________.
阶魅力圆”.“4阶魅力圆”中最多可有的等分点个数为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)= ln(a x)+bx在点(1,f(1))处的切线是y=0;
(I)求函数f(x)的极值;
(II)当![]() 恒成立时,求实数m的取值范围(e为自然对数的底数)
恒成立时,求实数m的取值范围(e为自然对数的底数)
查看答案和解析>>
科目: 来源: 题型:
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就.在“杨辉三角”中,已知第![]() 行的所有数字之和为
行的所有数字之和为![]() ,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,……,则此数列的前56项和为( )
,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,……,则此数列的前56项和为( )

A. 2060B. 2038C. 4084D. 4108
查看答案和解析>>
科目: 来源: 题型:
【题目】下列命题中正确的是( )
A. 有两个面平行,其余各面都是四边形的几何体叫棱柱
B. 有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱
C. 用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台
D. 有两个面平行,其余各面都是平行四边形的几何体叫棱柱
查看答案和解析>>
科目: 来源: 题型:
【题目】为了响应党的十九大所提出的教育教学改革,某校启动了数学教学方法的探索,学校将髙一年级部分生源情况基本相同的学生分成甲、乙两个班,每班40人,甲班按原有传统模式教学,乙班实施自主学习模式.经过一年的教学实验,将甲、乙两个班学生一年来的数学成绩取平均数,两个班学生的平均成绩均在[50,100],按照区间[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀,



![]() ,
,
(I)完成表格,并判断是否有90%以上的把握认为“数学成绩优秀与教学改革有关”

〔Ⅱ)从乙班[70,80),[80,90),[90,100]分数段中,按分层抽样随机抽取7名学生座谈,
从中选三位同学发言,记来自[80,90)发言的人数为随机变量x,求x的分布列和期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ax2﹣x﹣lnx,a∈R.
(1)当 ![]() 时,求函数f(x)的最小值;
时,求函数f(x)的最小值;
(2)若﹣1≤a≤0,证明:函数f(x)有且只有一个零点;
(3)若函数f(x)有两个零点,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com