
科目: 来源: 题型:
【题目】已知等比数列![]() 的公比
的公比![]() ,前
,前![]() 项和为
项和为![]() ,且满足
,且满足![]() .
.![]() ,
,![]() ,
,![]() 分别是一个等差数列的第1项,第2项,第5项.
分别是一个等差数列的第1项,第2项,第5项.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若![]() ,
,![]() 的前
的前![]() 项和为
项和为![]() ,且对任意的
,且对任意的![]() 满足
满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD= ![]() AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
AD.E为棱AD的中点,异面直线PA与CD所成的角为90°. 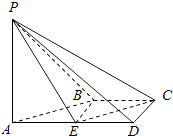
(1)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(2)若二面角P﹣CD﹣A的大小为45°,求直线PA与平面PCE所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(1)求C;
(2)若c= ![]() ,△ABC的面积为
,△ABC的面积为 ![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某科研小组研究发现:一棵水蜜桃树的产量![]() (单位:百千克)与肥料费用
(单位:百千克)与肥料费用![]() (单位:百元)满足如下关系:
(单位:百元)满足如下关系:![]() ,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)
,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)![]() 百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为
百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为![]() (单位:百元).
(单位:百元).
(1)求利润函数![]() 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(2)当投入的肥料费用为多少时,该水蜜桃树获得的利润最大?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一张坐标纸上已作出圆![]() 及点
及点![]() ,折叠此纸片,使
,折叠此纸片,使![]() 与圆周上某点
与圆周上某点![]() 重合,每次折叠都会留下折痕,设折痕与直线
重合,每次折叠都会留下折痕,设折痕与直线![]() 的交点为
的交点为![]() ,令点
,令点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.

(1)求曲线![]() 的方程;
的方程;
(2)若直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 、
、![]() 两点,且直线
两点,且直线![]() 与以
与以![]() 为直径的圆相切,若
为直径的圆相切,若![]() ,求
,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:吨)和年利润
(单位:吨)和年利润![]() (单位:万元)的影响。对近六年的年宣传费
(单位:万元)的影响。对近六年的年宣传费![]() 和年销售量
和年销售量![]() 的数据作了初步统计,得到如下数据:
的数据作了初步统计,得到如下数据:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年宣传费 | 38 | 48 | 58 | 68 | 78 | 88 |
年销售量 | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
经电脑拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() 即
即![]() 。对上述数据作了初步处理,得到相关的值如下表:
。对上述数据作了初步处理,得到相关的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)规定当产品的年销售量![]() (吨)与年宣传费
(吨)与年宣传费![]() (万元)的比值在区间
(万元)的比值在区间![]() 内时认为该年效益良好。现从这6年中任选2年,记其中选到效益良好年的数量为
内时认为该年效益良好。现从这6年中任选2年,记其中选到效益良好年的数量为![]() ,试求随机变量
,试求随机变量![]() 的分布列和期望。(其中
的分布列和期望。(其中![]() 为自然对数的底数,
为自然对数的底数, ![]() )
)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的正方形,侧面
是边长为2的正方形,侧面![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() ,侧面
,侧面![]() ⊥底面
⊥底面![]() .
.
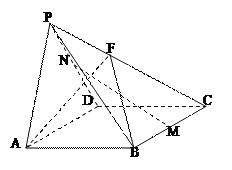
(1)若![]() 分别为棱
分别为棱![]() 的中点,求证:
的中点,求证:![]() ∥平面
∥平面![]() ;
;
(2)棱![]() 上是否存在一点
上是否存在一点![]() ,使二面角
,使二面角![]() 成
成![]() 角,若存在,求出
角,若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知符号函数sgnx= 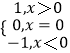 ,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),则( )
,f(x)是R上的增函数,g(x)=f(x)﹣f(ax)(a>1),则( )
A.sgn[g(x)]=sgnx
B.sgn[g(x)]=﹣sgnx
C.sgn[g(x)]=sgn[f(x)]
D.sgn[g(x)]=﹣sgn[f(x)]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com