【题目】函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分图象如图所示，则函数f（x）的解析式为 ．

【题目】在平面直角坐标系xOy中，直线l的参数方程为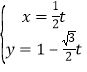(t为参数以坐标原点为极点，x轴正半轴为极轴建立极坐标系，圆C的极坐标方程为．

Ⅰ判断直线l与圆C的交点个数；

Ⅱ若圆C与直线l交于A，B两点，求线段AB的长度．

【题目】已知函数f(x)＝.

(1)判断函数f(x)的奇偶性；

(2)判断并用定义证明函数f(x)在其定义域上的单调性．

(3)若对任意的t1，不等式f()＋f()<0恒成立，求k的取值范围．

（1）应收集多少位女生样本数据？

（2）根据这300个样本数据，得到学生每周平均体育运动时间的频率分布直方图（如图所示），其中样本数据分组区间为：.估计该校学生每周平均体育运动时间超过4个小时的概率.

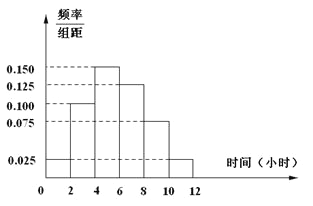
（3）在样本数据中，有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表，并判断是否有的把握认为“该校学生的每周平均体育运动时间与性别有关”.

附：

已知圆的参数方程为（为参数），若是圆与轴正半轴的交点，以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，设过点的圆的切线为.

（1）求直线的极坐标方程；

（2）求圆上到直线的距离最大的点的直角坐标.

【题目】设函数f（x）=2ax2+（a+4）x+lnx．
（1）若f（x）在x= 处的切线与直线4x+y=0平行，求a的值；
（2）讨论函数f（x）的单调区间；
（3）若函数y=f（x）的图象与x轴交于A，B两点，线段AB中点的横坐标为x0 ， 证明f′（x0）＜0．

【题目】已知函数，.

（1）求函数的单调区间；

（2）若，且关于的不等式恒成立，求实数的取值范围.

【题目】已知各项都是正数的数列{an}的前n项和为Sn ， Sn=an2+ an ， n∈N*
（1）求数列{an}的通项公式；
（2）设数列{bn}满足：b1=1，bn﹣bn﹣1=2an（n≥2），求数列{ }的前n项和Tn
（3）若Tn≤λ（n+4）对任意n∈N*恒成立，求λ的取值范围．

【题目】已知函数f（x）= x2﹣2ax+lnx（a∈R），x∈（1，+∞）．
（1）若函数f（x）有且只有一个极值点，求实数a的取值范围；
（2）对于函数f（x）、f1（x）、f2（x），若对于区间D上的任意一个x，都有f1（x）＜f（x）＜f2（x），则称函数f（x）是函数f1（x）、f2（x）在区间D上的一个“分界函数”．已知f1（x）=（1﹣a2）lnx，f2（x）=（1﹣a）x2 ， 问是否存在实数a，使得f（x）是函数f1（x）、f2（x）在区间（1，+∞）上的一个“分界函数”？若存在，求实数a的取值范围；若不存在，说明理由．

【题目】为美化环境，某市计划在以、两地为直径的半圆弧上选择一点建造垃圾处理厂（如图所示）.已知、两地的距离为，垃圾场对某地的影响度与其到该地的距离有关，对、两地的总影响度对地的影响度和对地影响度的和.记点到地的距离为，垃圾处理厂对、两地的总影响度为.统计调查表明：垃圾处理厂对地的影响度与其到地距离的平方成反比，比例系数为；对地的影响度与其到地的距离的平方成反比，比例系数为.当垃圾处理厂建在弧的中点时，对、两地的总影响度为.

（1）将表示成的函数；

（2）判断弧上是否存在一点，使建在此处的垃圾处理厂对、两地的总影响度最小？若存在，求出该点到地的距离；若不存在，说明理由.