
科目: 来源: 题型:
【题目】设数列{an}满足a1+a2+…+an+2n= ![]() (an+1+1),n∈N* , 且a1=1,求证:
(an+1+1),n∈N* , 且a1=1,求证:
(1)数列{an+2n}是等比数列;
(2)求数列{an}的前n项和Sn .
查看答案和解析>>
科目: 来源: 题型:
【题目】由代数式的乘法法则类比推导向量的数量积的运算法则:
①“mn=nm”类比得到“a·b=b·a”;
②“(m+n)t=mt+nt”类比得到“(a+b)·c=a·c+b·c”;
③“t≠0,mt=ntm=n”类比得到“c≠0,a·c=b·ca=b”;
④“|m·n|=|m|·|n|”类比得到“|a·b|=|a|·|b|”;
⑤“(m·n)t=m(n·t)”类比得到“(a·b)·c=a(b·c)”;
⑥“![]() ”类比得到
”类比得到![]() .以上的式子中,类比得到的结论正确的是________.
.以上的式子中,类比得到的结论正确的是________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知椭圆![]() 的离心率是
的离心率是![]() ,一个顶点是
,一个顶点是![]() .
.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() ,
,![]() 是椭圆
是椭圆![]() 上异于点
上异于点![]() 的任意两点,且
的任意两点,且![]() .试问:直线
.试问:直线![]() 是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由.
是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在某项娱乐活动的海选过程中评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰,成绩在![]() 内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.
内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.
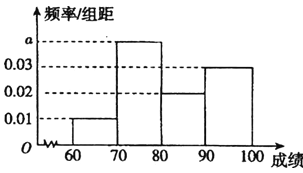
(1)已知成绩合格的200名参赛选手成绩的频率分布直方图如图,求a的值及估计这200名参赛选手的成绩平均数;
(2)根据已有的经验,参加复活赛的选手能够进入第二轮比赛的概率为![]() ,假设每名选手能否通过复活赛相互独立,现有3名选手进入复活赛,记这3名选手在复活赛中通过的人数为随机变量X,求X的分布列和数学期望.
,假设每名选手能否通过复活赛相互独立,现有3名选手进入复活赛,记这3名选手在复活赛中通过的人数为随机变量X,求X的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知中心在原点,焦点在x轴上的椭圆C的离心率为![]() ,点(0,
,点(0,![]() )是椭圆与y轴的一个交点.
)是椭圆与y轴的一个交点.
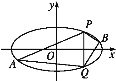
(1)求椭圆C的方程;
(2)直线x=2与椭圆交于P,Q两点,点P位于第一象限,A,B是椭圆上位于直线x=2两侧的动点;
①若直线AB的斜率为![]() ,求四边形APBQ面积的取值范围;
,求四边形APBQ面积的取值范围;
②当点A,B在椭圆上运动,且满足∠APQ=∠BPQ时,直线AB的斜率是否为定值?若是,求出此定值;若不是,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知四棱柱ABCD﹣A1B1C1D1的底面ABCD为正方形,AA1⊥AC,M、N分别为棱AA1、CC1的中点.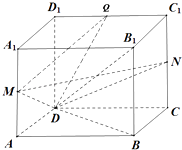
(1)求证:直线MN⊥平面B1BD;
(2)已知AA1=AB,AA1⊥AB,取线段C1D1的中点Q,求二面角Q﹣MD﹣N的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,离心率等于![]() ,它的一个顶点恰好是抛物线x2=8
,它的一个顶点恰好是抛物线x2=8![]() y的焦点.
y的焦点.
(1)求椭圆C的标准方程;
(2)直线x=﹣2与椭圆交于P,Q两点,A,B是椭圆上位于直线x=﹣2两侧的动点,若直线AB的斜率为![]() ,求四边形APBQ面积的最大值.
,求四边形APBQ面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点F为抛物线C:y2=4x的焦点,点P是准线l上的动点,直线PF交抛物线于A,B两点,若点P的纵坐标是m(m≠0),点D为准线l与x轴的交点.

(1)若m=2,求△DAB的面积;
(2)设![]() =λ
=λ![]() =μ
=μ![]() ,求证:λ+μ为定值.
,求证:λ+μ为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线l:(3+t)x﹣(t+1)y﹣4=0(t为参数)和圆C:x2+y2﹣6x﹣8y+16=0:
(1)t∈R时,证明直线l与圆C总相交:
(2)直线l被圆C截得弦长最短,求此弦长并求此时t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com