
科目: 来源: 题型:
【题目】已知圆C经过原点O(0,0)且与直线y=2x﹣8相切于点P(4,0).
(1)求圆C的方程;
(2)已知直线l经过点(4, 5),且与圆C相交于M,N两点,若|MN|=2,求出直线l的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 25 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |

(1)求出表中M,p及图中a的值;
(2)若该校高一学生有360人,试估计该校高一学生参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,请列举出所有基本事件,并求至多1人参加社区服务次数在区间[20,25)内的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,2acosC=bcosC+ccosB.
(1)求角C的大小;
(2)若c=![]() ,a2+b2=10,求△ABC的面积.
,a2+b2=10,求△ABC的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=aex﹣x(a∈R),其中e为自然对数的底数,e=2.71828…
(Ⅰ)判断函数f(x)的单调性,并说明理由
(Ⅱ)若x∈[1,2],不等式f(x)≥e﹣x恒成立,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (k
(k![]() R),且满足f(﹣1)=f(1).
R),且满足f(﹣1)=f(1).
(1)求k的值;
(2)若函数y=f(x)的图象与直线![]() 没有交点,求a的取值范围;
没有交点,求a的取值范围;
(3)若函数![]() ,x
,x![]() [0,log23],是否存在实数m使得h(x)最小值为0,若存在,求出m的值;若不存在,请说明理由.
[0,log23],是否存在实数m使得h(x)最小值为0,若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】设数列{an}的前n项和Sn满足:Sn=nan﹣2n(n﹣1),首项![]() =1.
=1.
(1)求数列{an}的通项公式;
(2)设数列![]() 的前n项和为Mn,求证:
的前n项和为Mn,求证:![]()
![]() Mn
Mn![]()
![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】设各项均为正数的数列{an}的前n项和为Sn , 且满足2 ![]() =an+1(n∈N*).
=an+1(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=(an+1)2 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目: 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,当x>0时,f(x)= ![]() x3+ax(a∈R),且曲线f(x)在x=
x3+ax(a∈R),且曲线f(x)在x= ![]() 处的切线与直线y=﹣
处的切线与直线y=﹣ ![]() x﹣1平行.
x﹣1平行.
(Ⅰ)求a的值及函数f(x)的解析式;
(Ⅱ)若函数y=f(x)﹣m在区间[﹣3, ![]() ]上有三个零点,求实数m的取值范围.
]上有三个零点,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】张三同学从7岁起到13岁每年生日时对自己的身高测量后记录如表:
年龄 (岁) | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
身高 (cm) | 121 | 128 | 135 | 141 | 148 | 154 | 160 |
(Ⅰ)求身高y关于年龄x的线性回归方程;
(Ⅱ)利用(Ⅰ)中的线性回归方程,分析张三同学7岁至13岁身高的变化情况,如17岁之前都符合这一变化,请预测张三同学15岁时的身高.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:![]() =
= 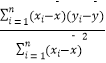 ,
, ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆C经过原点O(0,0)且与直线y=2x﹣8相切于点P(4,0).
(1)求圆C的方程;
(2)已知直线l经过点(4, 5),且与圆C相交于M,N两点,若|MN|=2,求出直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com