
科目: 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn+2=2an , 等差数列{bn}的前n项和为Tn , 且T2=S2=b3 .
(1)求数列{bn}的通项公式;
(2)令 ![]() ,求数列{cn}的前n项和Rn .
,求数列{cn}的前n项和Rn .
查看答案和解析>>
科目: 来源: 题型:
【题目】四棱锥P﹣ABCD中,底面ABCD为矩形, ![]() 为BC的中点,连接AE,BD,交点H,PH⊥平面ABCD,M为PD的中点.
为BC的中点,连接AE,BD,交点H,PH⊥平面ABCD,M为PD的中点. 
(1)求证:平面MAE⊥平面PBD;
(2)设PE=1,求二面角M﹣AE﹣C的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知向量 ![]() ,函数
,函数 ![]() ,若函数f(x)图象的两个相邻的对称轴间的距离为
,若函数f(x)图象的两个相邻的对称轴间的距离为 ![]() .
.
(1)求函数f(x)的单调增区间;
(2)在△ABC中,角A,B,C所对的边分别是a,b,c,若△ABC满足f(A)=1,a=3,BC边上的中线长为3,求△ABC的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】双十一期间某电商准备矩形促销市场调查,该电商决定活动,市场调查,该电商决定从2种服装商品,2种家电商品,3种日用商品中,选出3种商品进行促销活动.
(1)试求选出的3种商品中至多有一种是家电商品的概率;
(2)电商对选出的某商品采用促销方案是有奖销售,顾客购买该商品,一共有3次抽奖的机会,若中奖,则每次都活动数额为40元的奖券,假设顾客每次抽奖时中奖的概率都是 ![]() ,且每次中奖互不影响,设一位顾客中奖金额为随机变量ξ,求ξ的分布列和期望.
,且每次中奖互不影响,设一位顾客中奖金额为随机变量ξ,求ξ的分布列和期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】在实数集R中定义一种运算“*”,对任意a,b∈R,a*b为唯一确定的实数,且具有性质:
(Ⅰ)对任意a∈R,a*0=a;
(Ⅱ)对任意Ra,b∈R,a*b=ab+(a*0)+(b*0).
关于函数f(x)=(ex)* ![]() 的性质,有如下说法:①函数f(x)的最小值为3;②函数f(x)为偶函数;③函数f(x)的单调递增区间为(﹣∞,0].其中所有正确说法的序号为 .
的性质,有如下说法:①函数f(x)的最小值为3;②函数f(x)为偶函数;③函数f(x)的单调递增区间为(﹣∞,0].其中所有正确说法的序号为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)对定义域内R内的任意x都有f(x)=f(4﹣x),且当x≠2时,其导数f'(x)满足xf'(x)>2f'(x),若2<a<4,则( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b分别为16,20,则输出的a=( ) 
A.0
B.2
C.4
D.14
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=(x2﹣a)e1﹣x , g(x)=f(x)+ae1﹣x﹣a(x﹣1).
(1)讨论f(x)的单调性;
(2)当a=1时,求g(x)在( ![]() ,2)上的最大值;
,2)上的最大值;
(3)当f(x)有两个极值点x1 , x2(x1<x2)时,总有x2f(x1)≤λg′(x1),求实数λ的值(g′(x)为g(x)的导函数)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知DP⊥y轴,点D为垂足,点M在线段DP的延长线上,且满足|DP|=|PM|,当点P在圆x2+y2=3上运动时 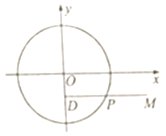
(1)求点M的轨迹C的方程;
(2)直线l:x=my+3(m≠0)交曲线C于A、B两点,设点B关于x轴的对称点为B1(点B1与点A不重合),且直线B1A与x轴交于点E. ①证明:点E是定点;
②△EAB的面积是否存在最大值?若存在,求出最大值,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}满足an+2= ![]() ,n∈N*,且a1=1,a2=2.
,n∈N*,且a1=1,a2=2.
(1)求数列{an}的通项公式;
(2)令bn=(﹣1)nanan+1 , n∈N*,求数列{bn}的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com