
科目: 来源: 题型:
【题目】对函数f(x),如果存在x0≠0使得f(x0)=﹣f(﹣x0),则称(x0 , f(x0))与(﹣x0 , f(﹣x0))为函数图象的一组奇对称点.若f(x)=ex﹣a(e为自然数的底数)存在奇对称点,则实数a的取值范围是( )
A.(﹣∞,1)
B.(1,+∞)
C.(e,+∞)
D.[1,+∞)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知集合Rn={X|X=(x1 , x2 , …,xn),xi∈{0,1},i=1,2,…,n}(n≥2).对于A=(a1 , a2 , …,an)∈Rn , B=(b1 , b2 , …,bn)∈Rn , 定义A与B之间的距离为d(A,B)=|a1﹣b1|+|a2﹣b2|+…|an﹣bn|= ![]() .
.
(Ⅰ)写出R2中的所有元素,并求两元素间的距离的最大值;
(Ⅱ)若集合M满足:MR3 , 且任意两元素间的距离均为2,求集合M中元素个数的最大值并写出此时的集合M;
(Ⅲ)设集合PRn , P中有m(m≥2)个元素,记P中所有两元素间的距离的平均值为 ![]() ,证明
,证明 ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆E: ![]() +
+ ![]() =1(a>b>0)过点(0,1),且离心率为
=1(a>b>0)过点(0,1),且离心率为 ![]() .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设直线l:y= ![]() +m与椭圆E交于A、C两点,以AC为对角线作正方形ABCD,记直线l与x轴的交点为N,问B,N两点间距离是否为定值?如果是,求出定值;如果不是,请说明理由.
+m与椭圆E交于A、C两点,以AC为对角线作正方形ABCD,记直线l与x轴的交点为N,问B,N两点间距离是否为定值?如果是,求出定值;如果不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=1nx.
(Ⅰ)求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求证:当x>0时, ![]() ;
;
(Ⅲ)若x﹣1>a1nx对任意x>1恒成立,求实数a的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑. 如图,在阳马P﹣ABCD中,侧棱PD⊥底面ABCD,且PD=CD,E为PC中点,点F在PB上,且PB⊥平面DEF,连接BD,BE.
(Ⅰ)证明:DE⊥平面PBC;
(Ⅱ)试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
(Ⅲ)已知AD=2, ![]() ,求二面角F﹣AD﹣B的余弦值.
,求二面角F﹣AD﹣B的余弦值.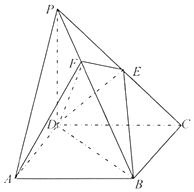
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市从现有甲、乙两种酸奶的日销售量(单位:箱)的1200个数据(数据均在区间(0,50]内)中,按照5%的比例进行分层抽样,统计结果按(0,10],(10,20],(20,30],(30,40],(40,50]分组,整理如下图: 
(Ⅰ)写出频率分布直方图(图乙)中a的值;记所抽取样本中甲种酸奶与乙种酸奶日销售量的方差分别为 ![]() ,
, ![]() ,试比较
,试比较 ![]() 与
与 ![]() 的大小(只需写出结论);
的大小(只需写出结论);
(Ⅱ)从甲种酸奶日销售量在区间(0,20]的数据样本中抽取3个,记在(0,10]内的数据个数为X,求X的分布列;
(Ⅲ)估计1200个日销售量数据中,数据在区间(0,10]中的个数.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国南宋数学家秦九韶(约公元1202﹣1261年)给出了求n(n∈N*)次多项式anxn+an﹣1xn﹣1+…+a1x+a0 , 当x=x0时的值的一种简捷算法.该算法被后人命名为“秦九韶算法”,例如,可将3次多项式改写为a3x3+a2x2+a1x+a0=((a3x+a2)x+a1)x+a0 , 然后进行求值.运行如图所示的程序框图,能求得多项式( )的值.
A.x4+x3+2x2+3x+4
B.x4+2x3+3x2+4x+5
C.x3+x2+2x+3
D.x3+2x2+3x+4
查看答案和解析>>
科目: 来源: 题型:
【题目】[选修4-5:不等式选讲]已知函数f(x)=2|x+1|+|x﹣2|的最小值为m.
(Ⅰ)求实数m的值;
(Ⅱ)若a,b,c均为正实数,且满足a+b+c=m,求证: ![]() +
+ ![]() +
+ ![]() ≥3.
≥3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com