
科目: 来源: 题型:
【题目】在平面直角坐标系xoy中,过椭圆 ![]() 右焦点的直线
右焦点的直线 ![]() 交椭圆C于M,N两点,P为M,N的中点,且直线OP的斜率为
交椭圆C于M,N两点,P为M,N的中点,且直线OP的斜率为 ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设另一直线l与椭圆C交于A,B两点,原点O到直线l的距离为 ![]() ,求△AOB面积的最大值.
,求△AOB面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列命题中,错误的命题个数有( )
①![]() 是
是![]() 为奇函数的必要非充分条件;
为奇函数的必要非充分条件;
②函数![]() 是偶函数;
是偶函数;
③函数![]() 的最小值是
的最小值是![]() ;
;
④函数![]() 的定义域为
的定义域为![]() ,且对其内任意实数
,且对其内任意实数![]() 、
、![]() 均有:
均有:![]() ,则
,则![]() 在
在![]() 上是减函数.
上是减函数.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如甲图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起到△D1AE位置,使平面D1AE⊥平面ABCE,得到乙图所示的四棱锥D1﹣ABCE.
(Ⅰ)求证:BE⊥平面D1AE;
(Ⅱ)求二面角A﹣D1E﹣C的余弦值.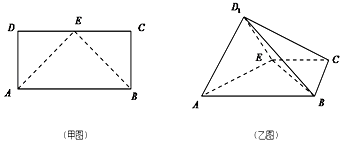
查看答案和解析>>
科目: 来源: 题型:
【题目】在某单位的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以x(单位:个,60≤x≤110)表示面包的需求量,T(单位:元)表示利润.
(Ⅰ)求T关于x的函数解析式;
(Ⅱ)根据直方图估计利润T不少于100元的概率;
(Ⅲ)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中间值的概率(例如:若需求量x∈[60,70),则取x=65,且x=65的概率等于需求量落入[60,70)的频率),求T的分布列和数学期望.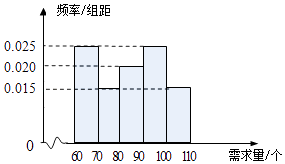
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,a,b,c成等比数列,且a2﹣c2=ac﹣bc.
(Ⅰ)求∠A的大小;
(Ⅱ)若a= ![]() ,且sinA+sin(B﹣C)=2sin2C,求△ABC的面积.
,且sinA+sin(B﹣C)=2sin2C,求△ABC的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=m﹣|x﹣2|,m∈R,且f(x+2)≥0的解集为[﹣3,3].
(Ⅰ)解不等式:f(x)+f(x+2)>0;
(Ⅱ)若a,b,c均为正实数,且满足a+b+c=m,求证: ![]() ≥3.
≥3.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xoy中,已知点P(0, ![]() ),曲线C的参数方程为
),曲线C的参数方程为 ![]() (φ为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ=
(φ为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ= ![]() .
.
(Ⅰ)判断点P与直线l的位置关系并说明理由;
(Ⅱ)设直线l与曲线C的两个交点分别为A,B,求 ![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=x2+aln(x+1),a∈R.
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)若函数f(x)有两个极值点x1 , x2 , 且x1<x2 , 求证:f(x2)≥( ![]() ﹣1)x2 .
﹣1)x2 .
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xoy中,过椭圆 ![]() 右焦点的直线
右焦点的直线 ![]() 交椭圆C于M,N两点,P为M,N的中点,且直线OP的斜率为
交椭圆C于M,N两点,P为M,N的中点,且直线OP的斜率为 ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设另一直线l与椭圆C交于A,B两点,原点O到直线l的距离为 ![]() ,求△AOB面积的最大值.
,求△AOB面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如甲图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起到△D1AE位置,使平面D1AE⊥平面ABCE,得到乙图所示的四棱锥D1﹣ABCE.
(Ⅰ)求证:BE⊥平面D1AE;
(Ⅱ)求二面角A﹣D1E﹣C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com