
科目: 来源: 题型:
【题目】已知向量 ![]() =(sinx,1),
=(sinx,1), ![]() =(2cosx,3),x∈R.
=(2cosx,3),x∈R.
(1)当 ![]() =λ
=λ ![]() 时,求实数λ和tanx的值;
时,求实数λ和tanx的值;
(2)设函数f(x)= ![]()
![]() ,求f(x)的最小正周期和单调递减区间.
,求f(x)的最小正周期和单调递减区间.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,平面PAB⊥平面ABC,△PAB是等边三角形,AC⊥BC,且AC=BC=2,O、D分别是AB,PB的中点. 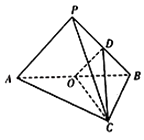
(1)求证:PA∥平面COD;
(2)求三棱锥P﹣ABC的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=2+ ![]() 的图象经过点(2,3),a为常数.
的图象经过点(2,3),a为常数.
(1)求a的值和函数f(x)的定义域;
(2)用函数单调性定义证明f(x)在(a,+∞)上是减函数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}的各项均为正数,其前n项和为Sn , 且an2+an=2Sn , n∈N* .
(1)求a1及an;
(2)求满足Sn>210时n的最小值;
(3)令bn=4 ![]() ,证明:对一切正整数n,都有
,证明:对一切正整数n,都有 ![]() +
+ ![]() +
+ ![]() ++
++ ![]() <
< ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知f(x)=|x+a|,g(x)=|x+3|﹣x,记关于x的不等式f(x)<g(x)的解集为M.
(1)若a﹣3∈M,求实数a的取值范围;
(2)若[﹣1,1]M,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为  (t为参数).以O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为ρ=2acosθ(a>0),且曲线C与直线l有且仅有一个公共点.
(t为参数).以O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为ρ=2acosθ(a>0),且曲线C与直线l有且仅有一个公共点.
(Ⅰ)求a;
(Ⅱ)设A、B为曲线C上的两点,且∠AOB= ![]() ,求|OA|+|OB|的最大值.
,求|OA|+|OB|的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=2lnx+x2+(a﹣1)x﹣a,(a∈R),当x≥1时,f(x)≥0恒成立.
(1)求实数a的取值范围;
(2)若正实数x1、x2(x1≠x2)满足f(x1)+f(x2)=0,证明:x1+x2>2.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A与点A′在x轴上,且关于y轴对称,过点A′垂直于x轴的直线与抛物线y2=2x交于两点B,C,点D为线段AB 上的动点,点E在线段AC上,满足 ![]() .
.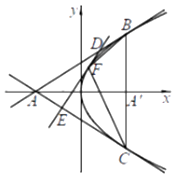
(1)求证:直线DE与此抛物线有且只有一个公共点;
(2)设直线DE与此抛物线的公共点F,记△BCF与△ADE的面积分别为S1、S2 , 求 ![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图多面体ABCD中,面ABCD为正方形,棱长AB=2,AE=3,DE= ![]() ,二面角E﹣AD﹣C的余弦值为
,二面角E﹣AD﹣C的余弦值为 ![]() ,且EF∥BD.
,且EF∥BD. 
(1)证明:面ABCD⊥面EDC;
(2)若直线AF与平面ABCD所成角的正弦值为 ![]() ,求二面角AF﹣E﹣DC的余弦值.
,求二面角AF﹣E﹣DC的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】习大大构建的“一带一路”经济带的发展规划已经得到了越来越多相关国家的重视和参与.某市顺潮流、乘东风,闻迅而动,决定利用旅游资源优势,撸起袖子大干一场.为了了解游客的情况,以便制定相应的策略.在某月中随机抽取甲、乙两个景点各10天的游客数,画出茎叶图如下: 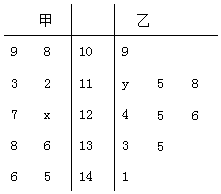
(1)若景点甲中的数据的中位数是125,景点乙中的数据的平均数是124,求x,y的值;
(2)若将图中景点甲中的数据作为该景点较长一段时期内的样本数据.今从这段时期中任取4天,记其中游客数超过120人的天数为ξ,求概率P(ξ≤2);
(3)现从上图的共20天的数据中任取2天的数据(甲、乙两景点中各取1天),记其中游客数不低于115且不高于125人的天数为η,求η的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com