
科目: 来源: 题型:
【题目】已知m是一个给定的正整数,m≥3,设数列{an}共有m项,记该数列前i项a1 , a2 , …,ai中的最大项为Ai , 该数列后m﹣i项ai+1 , ai+2 , …,am中的最小项为Bi , ri=Ai﹣Bi(i=1,2,3,…,m﹣1);
(1)若数列{an}的通项公式为 ![]() (n=1,2,…,m),求数列{ri}的通项公式;
(n=1,2,…,m),求数列{ri}的通项公式;
(2)若数列{an}满足a1=1,r1=﹣2(i=1,2,…,m﹣1),求数列{an}的通项公式;
(3)试构造项数为m的数列{an},满足an=bn+cn , 其中{bn}是公差不为零的等差数列,{cn}是等比数列,使数列{ri}是单调递增的,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,设点M(x0 , y0)是椭圆C: ![]() +y2=1上一点,从原点O向圆M:(x﹣x0)2+(y﹣y0)2=r2作两条切线分别与椭圆C交于点P,Q.直线OP,OQ的斜率分别记为k1 , k2
+y2=1上一点,从原点O向圆M:(x﹣x0)2+(y﹣y0)2=r2作两条切线分别与椭圆C交于点P,Q.直线OP,OQ的斜率分别记为k1 , k2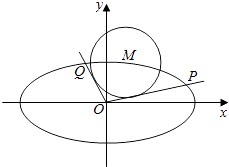
(1)若圆M与x轴相切于椭圆C的右焦点,求圆M的方程;
(2)若r= ![]() ,①求证:k1k2=﹣
,①求证:k1k2=﹣ ![]() ;②求OPOQ的最大值.
;②求OPOQ的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,侧棱PA⊥平面ABCD,E为AD的中点,BE∥CD,BE⊥AD,PA=AE=BE=2,CD=1; 
(1)求二面角C﹣PB﹣E的余弦值;
(2)在线段PE上是否存在点M,使得DM∥平面PBC?若存在,求出点M的位置,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,O为总信号源点,A,B,C是三个居民区,已知A,B都在O的正东方向上,OA=10km,OB=20km,C在O的北偏西45°方向上,CO=5 ![]() km.
km. 
(1)求居民区A与C的距离;
(2)现要经过点O铺设一条总光缆直线EF(E在直线OA的上方),并从A,B,C分别铺设三条最短分光缆连接到总光缆EF.假设铺设每条分光缆的费用与其长度的平方成正比,比例系数为m(m为常数).设∠AOE=θ(0≤θ<π),铺设三条分光缆的总费用为w(元). ①求w关于θ的函数表达式;
②求w的最小值及此时tanθ的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】若向量 ![]() ,在函数
,在函数 ![]() 的图象中,对称中心到对称轴的最小距离为
的图象中,对称中心到对称轴的最小距离为 ![]() ,且当
,且当 ![]() 的最大值为1.
的最大值为1.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数f(x)的单调递增区间.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知四数a1 , a2 , a3 , a4依次成等比数列,且公比q不为1.将此数列删去一个数后得到的数列(按原来的顺序)是等差数列,则正数q的取值集合是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】对数列{an},如果k∈N*及λ1 , λ2 , …,λk∈R,使an+k=λ1an+k﹣1+λ2an+k﹣2+…+λkan成立,其中n∈N* , 则称{an}为k阶递归数列.给出下列三个结论: ①若{an}是等比数列,则{an}为1阶递归数列;
②若{an}是等差数列,则{an}为2阶递归数列;
③若数列{an}的通项公式为 ![]() ,则{an}为3阶递归数列.
,则{an}为3阶递归数列.
其中,正确结论的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目: 来源: 题型:
【题目】已知复数z1=m+ni(m,n∈R),z=x+yi(x,y∈R),z2=2+4i且 ![]() .
.
(1)若复数z1对应的点M(m,n)在曲线 ![]() 上运动,求复数z所对应的点P(x,y)的轨迹方程;
上运动,求复数z所对应的点P(x,y)的轨迹方程;
(2)将(1)中的轨迹上每一点按向量 ![]() 方向平移
方向平移 ![]() 个单位,得到新的轨迹C,求C的轨迹方程;
个单位,得到新的轨迹C,求C的轨迹方程;
(3)过轨迹C上任意一点A(异于顶点)作其切线,交y轴于点B,求证:以线段AB为直径的圆恒过一定点,并求出此定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com