
【题目】将函数 ![]() 的图象向左平移m(m>0)个单位长度,得到的函数y=f(x)在区间
的图象向左平移m(m>0)个单位长度,得到的函数y=f(x)在区间 ![]() 上单调递减,则m的最小值为 .
上单调递减,则m的最小值为 .
【答案】![]()
【解析】解:将函数 ![]() 的图象向左平移m(m>0)个单位长度,可得y=sin(2x+2m+
的图象向左平移m(m>0)个单位长度,可得y=sin(2x+2m+ ![]() )的图象,
)的图象,
由2kπ+ ![]() ≤2x+2m+
≤2x+2m+ ![]() ≤2kπ+
≤2kπ+ ![]() ,可得kπ﹣m+
,可得kπ﹣m+ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,
,
故函数y=sin(2x+2m+ ![]() )的减区间为[kπ﹣m+
)的减区间为[kπ﹣m+ ![]() ,kπ﹣m+
,kπ﹣m+ ![]() ],k∈Z.
],k∈Z.
∵得到的函数y=f(x)在区间 ![]() 上单调递减,∴kπ﹣m+
上单调递减,∴kπ﹣m+ ![]() ≤﹣
≤﹣ ![]() ,
, ![]() ≤kπ﹣m+
≤kπ﹣m+ ![]() ,
,
求得 m≥kπ+ ![]() ,且m≤kπ+
,且m≤kπ+ ![]() ,∴m的最小值为
,∴m的最小值为 ![]() ,
,
所以答案是: ![]() .
.
【考点精析】利用函数y=Asin(ωx+φ)的图象变换对题目进行判断即可得到答案,需要熟知图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】已知三棱锥A﹣BCD的所有棱长都相等,若AB与平面α所成角等于 ![]() ,则平面ACD与平面α所成角的正弦值的取值范围是( )
,则平面ACD与平面α所成角的正弦值的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,1]
,1]
C.[ ![]() ﹣
﹣ ![]() ,
, ![]() +
+ ![]() ]
]
D.[ ![]() ﹣
﹣ ![]() ,1]
,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以O为极点,x轴非负半轴为极轴建立极坐标系,取相同的长度单位,已知曲线C的极坐标方程为ρ=2 ![]() sinθ,直线l的参数方程为
sinθ,直线l的参数方程为  (t为参数).
(t为参数).
(Ⅰ)写出曲线C的直角坐标方程和直线l的普通方程.
(Ⅱ)若P(3, ![]() ),直线l与曲线C相交于M,N两点,求|PM|+|PN|的值.
),直线l与曲线C相交于M,N两点,求|PM|+|PN|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知球内接四棱锥P﹣ABCD的高为3,AC,BC相交于O,球的表面积为 ![]() ,若E为PC中点.
,若E为PC中点. 
(1)求证:OE∥平面PAD;
(2)求二面角A﹣BE﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体ABCDE中,△ABC是正三角形,EA和DC都垂直于平面ABC,且EA=AB=2a,DC=a,F、G分别为EB和AB的中点. 
(1)求证:FD∥平面ABC;
(2)求二面角B﹣FC﹣G的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,设点M(x0 , y0)是椭圆C: ![]() +y2=1上一点,从原点O向圆M:(x﹣x0)2+(y﹣y0)2=r2作两条切线分别与椭圆C交于点P,Q.直线OP,OQ的斜率分别记为k1 , k2
+y2=1上一点,从原点O向圆M:(x﹣x0)2+(y﹣y0)2=r2作两条切线分别与椭圆C交于点P,Q.直线OP,OQ的斜率分别记为k1 , k2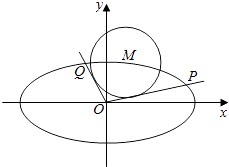
(1)若圆M与x轴相切于椭圆C的右焦点,求圆M的方程;
(2)若r= ![]() ,①求证:k1k2=﹣
,①求证:k1k2=﹣ ![]() ;②求OPOQ的最大值.
;②求OPOQ的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,D是直角△ABC斜边BC上一点,AC= ![]() DC.
DC. 
(I)若∠DAC=30°,求角B的大小;
(Ⅱ)若BD=2DC,且AD=2 ![]() ,求DC的长.
,求DC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形.
的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点M分别作直线MA,MB交椭圆于A,B两点,设两直线的斜率分别为k1 , k2 , 且k1+k2=8,证明:直线AB过定点( ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】考拉兹猜想又名3n+1猜想,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能得到1.阅读如图所示的程序框图,运行相应程序,输出的结果i=( ) 
A.4
B.5
C.6
D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com