
科目: 来源: 题型:
【题目】已知椭圆C:x2+4y2=4.
(1)求椭圆C的离心率;
(2)椭圆C的长轴的两个端点分别为A,B,点P在直线x=1上运动,直线PA,PB分别与椭圆C相交于M,N两个不同的点,求证:直线MN与x轴的交点为定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=x﹣1+aex .
(1)若曲线y=f(x)在点(1,f(1))处的切线平行于x轴,求a的值;
(2)求f(x)的极值;
(3)当a=1时,曲线y=f(x)与直线y=kx﹣1没有公共点,求k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在边长为2的菱形ABCD中,∠BAD=60°,将△BCD沿对角线BD折起到△B'CD的位置,使平面BC'D⊥平面ABD,E是BD的中点,FA⊥平面ABD,且FA=2 ![]() ,如图2.
,如图2. 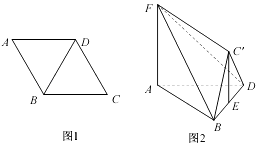
(1)求证:FA∥平面BC'D;
(2)求平面ABD与平面FBC'所成角的余弦值;
(3)在线段AD上是否存在一点M,使得C'M⊥平面FBC?若存在,求 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学高一、高二年级各有8个班,学校调查了春学期各班的文学名著阅读量(单位:本),并根据调查结果,得到如下所示的茎叶图: 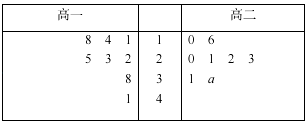
为鼓励学生阅读,在高一、高二两个两个年级中,学校将阅读量高于本年级阅读量平均数的班级命名为该年级的“书香班级”.
(1)当a=4时,记高一年级“书香班级”数为m,高二年级的“书香班级”数为n,比较m,n的大小关系;
(2)在高一年级8个班级中,任意选取两个,求这两个班级均是“书香班级”的概率;
(3)若高二年级的“书香班级”数多于高一年级的“书香班级”数,求a的值(只需写出结论)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=sin(ωx﹣ ![]() )(ω>0)的图象与x轴的相邻两个交点的距离为
)(ω>0)的图象与x轴的相邻两个交点的距离为 ![]() .
.
(1)求w的值;
(2)设函数g(x)=f(x)+2cos2x﹣1,求g(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,他在《数学九章》中提出的多项式的秦九韶算法,至今仍是比较先进的算法,如图是事项该算法的程序框图,执行该程序框图,若输入n,x的值分别为4,2,则输出v的值为( ) 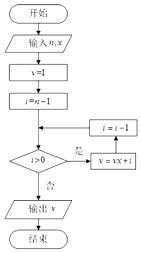
A.5
B.12
C.25
D.50
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数 ![]() (a>0). (Ⅰ)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(a>0). (Ⅰ)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若 ![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(Ⅲ)证明:总存在x0 , 使得当x∈(x0 , +∞),恒有f(x)<1.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C: ![]() ,点P(4,0),过右焦点F作与y轴不垂直的直线l交椭圆C于A,B两点. (Ⅰ)求椭圆C的离心率;
,点P(4,0),过右焦点F作与y轴不垂直的直线l交椭圆C于A,B两点. (Ⅰ)求椭圆C的离心率;
(Ⅱ)求证:以坐标原点O为圆心与PA相切的圆,必与直线PB相切.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为研究学生语言学科的学习情况,现对高二200名学生英语和语文某次考试成绩进行抽样分析.将200名学生编号为001,002,…,200,采用系统抽样的方法等距抽取10名学生,将10名学生的两科成绩(单位:分)绘成折线图如下: 
(Ⅰ)若第一段抽取的学生编号是006,写出第五段抽取的学生编号;
(Ⅱ)在这两科成绩差超过20分的学生中随机抽取2人进行访谈,求2人成绩均是语文成绩高于英语成绩的概率;
(Ⅲ)根据折线图,比较该校高二年级学生的语文和英语两科成绩,写出你的结论和理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PD⊥平面PAB,AD∥BC,BC=CD= ![]() AD,E,F分别为线段AD,PD的中点.
AD,E,F分别为线段AD,PD的中点. 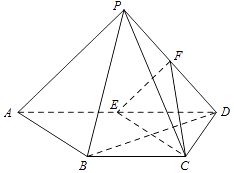
(Ⅰ)求证:CE∥平面PAB;
(Ⅱ)求证:PD⊥平面CEF;
(Ⅲ)写出三棱锥D﹣CEF与三棱锥P﹣ABD的体积之比.(结论不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com