
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以
),以![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】【2018山西太原市高三3月模拟】已知椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,右焦点为
,右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(I)求椭圆方程;
(II)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,已知直线
两点,已知直线![]() 与
与![]() 相交于点
相交于点![]() ,证明:点
,证明:点![]() 在定直线上,并求出定直线的方程.
在定直线上,并求出定直线的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校倡导为特困学生募捐,要求在自动购水机处每购买一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出矿泉水箱数和收入情况,列表如下:
售出水量 | 7 | 6 | 6 | 5 | 6 |
收入 | 165 | 142 | 148 | 125 | 150 |
学校计划将捐款以奖学金的形式奖励给品学兼优的特困生,规定:特困生综合考核前20名,获一等奖学金500元;综合考核21-50名,获二等奖学金300元;综合考核50名以后的不获得奖学金.
(1)若![]() 与
与![]() 成线性相关,则某天售出9箱水时,预计收入为多少元?
成线性相关,则某天售出9箱水时,预计收入为多少元?
(2)甲乙两名学生获一等奖学金的概率均为![]() ,获二等奖学金的概率均为
,获二等奖学金的概率均为![]() ,不获得奖学金的概率均为
,不获得奖学金的概率均为![]() ,已知甲乙两名学生获得哪个等级的奖学金相互独立,求甲乙两名学生所获得奖学金之和
,已知甲乙两名学生获得哪个等级的奖学金相互独立,求甲乙两名学生所获得奖学金之和![]() 的分布列及数学期望;
的分布列及数学期望;
附:回归方程![]() ,其中
,其中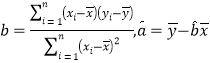 .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 上,
上, ![]() 为椭圆
为椭圆![]() 的右焦点,
的右焦点, ![]() 分别为椭圆
分别为椭圆![]() 的左,右两个顶点.若过点
的左,右两个顶点.若过点![]() 且斜率不为0的直线
且斜率不为0的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且线段
两点,且线段![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与
与![]() 相交于点
相交于点![]() ,证明:
,证明: ![]() 三点共线.
三点共线.
查看答案和解析>>
科目: 来源: 题型:
【题目】以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为:
的极坐标方程为:![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,直线
中,直线![]() 的方程为
的方程为 (
(![]() 为参数).
为参数).
(1)求曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() ,
,![]() 两点的距离.
两点的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知某班的50名学生进行不记名问卷调查,内容为本周使用手机的时间长,如表:
时间长(小时) |
|
|
|
|
|
女生人数 | 4 | 11 | 3 | 2 | 0 |
男生人数 | 3 | 17 | 6 | 3 | 1 |
(1)求这50名学生本周使用手机的平均时间长;
(2)时间长为![]() 的7名同学中,从中抽取两名,求其中恰有一个女生的概率;
的7名同学中,从中抽取两名,求其中恰有一个女生的概率;
(3)若时间长为![]() 被认定“不依赖手机”,
被认定“不依赖手机”,![]() 被认定“依赖手机”,根据以上数据完成
被认定“依赖手机”,根据以上数据完成![]() 列联表:
列联表:
不依赖手机 | 依赖手机 | 总计 | |
女生 | |||
男生 | |||
总计 |
能否在犯错概率不超过0.15的前提下,认为学生的性别与依赖手机有关系?
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】【2018湖南(长郡中学、株洲市第二中学)、江西(九江一中)等十四校高三第一次联考】已知函数![]() (其中
(其中![]() 且
且![]() 为常数,
为常数, ![]() 为自然对数的底数,
为自然对数的底数, ![]() ).
).
(Ⅰ)若函数![]() 的极值点只有一个,求实数
的极值点只有一个,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)当![]() 时,若
时,若![]() (其中
(其中![]() )恒成立,求
)恒成立,求![]() 的最小值
的最小值![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com