【题目】已知椭圆的左焦点为，上顶点为为坐标原点，椭圆的离心率且的面积为.

（1）求椭圆的方程；

（2）设线段的中点为，经过的直线与椭圆交于两点， ，若点关于轴的对称点在直线上，求直线方程.

【题目】某市甲水厂每天生产万吨的生活用水，其每天固定生产成本为万元，居民用水的税费价格为每吨元，该市居民每天用水需求量是在（单位：万吨）内的随机数，经市场调查，该市每天用水需求量的频率分布直方图如图所示，设（单位：万吨， ）表示该市一天用水需求量（单位：万元）表示甲水厂一天销售生活用水的利润（利润=税费收入-固定生产成本），注：当该市用水需求量超过万吨时，超过的部分居民可以用其他水厂生产的水，甲水厂只收成本厂供应的税费，该市每天用水需求量的概率用频率估计.

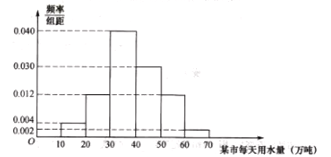
（1）求的值，并直接写出表达式；

（2）求甲水厂每天的利润不少于万元的概率.

【题目】如图所示，在四棱锥中， ,底面为梯形， 且平面.

（1）证明：平面平面；

（2）当异面直线与所成角为时，求四棱锥的体积.

在极坐标系中，曲线的极坐标方程为，以极点为原点，极轴为轴的非负半轴建立平面直角坐标系，直线的参数方程为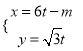（为参数， ）.

（1）求曲线的直角坐标方程和直线的普通方程；

（2）若曲线上的动点到直线的最大距离为，求的值.

【题目】用,,表示空间中三条不同的直线,表示平面, 给出下列命题:

① 若,, 则∥; ② 若∥,∥, 则∥;

③ 若∥,∥, 则∥; ④ 若 , , 则∥.

其中真命题的序号是（ ）

A. ①② B. ②③ C. ①④ D. ②④

【题目】先后2次抛掷一枚骰子，将得到的点数分别记为，.

（1）求直线与圆相切的概率；

（2）将，，5的值分别作为三条线段的长，求这三条线段能围成等腰三角形的概率.

【题目】已知函数，其中为自然对数的底数.

（1）求证：当时，对任意都有；

（2）若函数有两个极值点，求实数的取值范围.

【题目】某企业准备推出一种花卉植物用于美化城市环境，为评估花卉的生长水平，现对该花卉植株的高度（单位：厘米）进行抽查，所得数据分组为，据此制作的频率分布直方图如图所示.

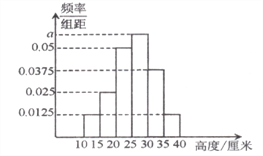
（1）求出直方图中的值；

（2）利用直方图估算花卉植株高度的中位数；

（3）若样本容量为32，现准备从高度在的植株中继续抽取2颗做进一步调查，求抽取植株来自同一组的概率.

【题目】已知函数

(1)求函数在区间上的值域

(2)把函数图象所有点的上横坐标缩短为原来的倍，再把所得的图象向左平移个单位长度，再把所得的图象向下平移1个单位长度，得到函数， 若函数关于点对称

（i）求函数的解析式；

（ii）求函数单调递增区间及对称轴方程.

【题目】如图为半圆的直径，点是半圆弧上的两点， ， ．曲线经过点，且曲线上任意点满足： 为定值.

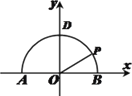
（Ⅰ）求曲线的方程；

（Ⅱ）设过点的直线与曲线交于不同的两点，求面积最大时的直线的方程．