
科目: 来源: 题型:
【题目】某学校课题组为了研究学生的数学成绩与学生细心程度的关系,在本校随机调查了100名学生进行研究.研究结果表明:在数学成绩及格的60名学生中有45人比较细心,另外15人比较粗心;在数学成绩不及格的40名学生中有10人比较细心,另外30人比较粗心.
(I)试根据上述数据完成![]() 列联表:
列联表:

(II)能否在犯错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系?
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: ,其中
,其中![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解人们对“![]() 年
年![]() 月在北京召开的第十三届全国人民代表大会第二次会议和政协第十三届全国委员会第二次会议”的关注度,某部门从年龄在
月在北京召开的第十三届全国人民代表大会第二次会议和政协第十三届全国委员会第二次会议”的关注度,某部门从年龄在![]() 岁到
岁到![]() 岁的人群中随机调查了
岁的人群中随机调查了![]() 人,并得到如图所示的年龄频率分布直方图,在这
人,并得到如图所示的年龄频率分布直方图,在这![]() 人中关注度非常髙的人数与年龄的统计结果如表所示:
人中关注度非常髙的人数与年龄的统计结果如表所示:
年龄 | 关注度非常高的人数 |
|
|
|
|
|
|
|
|
|
|

(1)由频率分布直方图,估计这![]() 人年龄的中位数和平均数;
人年龄的中位数和平均数;
(2)根据以上统计数据填写下面的![]() 列联表,据此表,能否在犯错误的概率不超过
列联表,据此表,能否在犯错误的概率不超过![]() 的前提下,认为以
的前提下,认为以![]() 岁为分界点的不同人群对“两会”的关注度存在差异?
岁为分界点的不同人群对“两会”的关注度存在差异?
(3)按照分层抽样的方法从年龄在![]() 岁以下的人中任选六人,再从六人中随机选两人,求两人中恰有一人年龄在
岁以下的人中任选六人,再从六人中随机选两人,求两人中恰有一人年龄在![]() 岁以下的概率是多少.
岁以下的概率是多少.
|
| 总计 | |
非常高 | |||
一般 | |||
总计 |
参考数据:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,已知直线
轴正半轴为极轴,建立极坐标系,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程,并指出该曲线是什么曲线;
的直角坐标方程,并指出该曲线是什么曲线;
(2)若直线![]() 与曲线
与曲线![]() 的交点分别为
的交点分别为![]() ,求
,求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 也为抛物线
也为抛物线![]() 的焦点.(1)若
的焦点.(1)若![]() 为椭圆
为椭圆![]() 上两点,且线段
上两点,且线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(2)若过椭圆![]() 的右焦点
的右焦点![]() 作两条互相垂直的直线分别交椭圆于
作两条互相垂直的直线分别交椭圆于![]() 和
和![]() ,设线段
,设线段![]() 的长分别为
的长分别为![]() ,证明
,证明![]() 是定值.
是定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某翻译处有8名翻译,其中有小张等3名英语翻译,小李等3名日语翻译,另外2名既能翻译英语又能翻译日语,现需选取5名翻译参加翻译工作,3名翻译英语,2名翻译日语,且小张与小李恰有1人选中,则有____种不同选取方法.
查看答案和解析>>
科目: 来源: 题型:
【题目】平顶山市公安局交警支队依据《中华人民共和国道路交通安全法》第![]() 条规定:所有主干道路凡机动车途经十字口或斑马线,无论转弯或者直行,遇有行人过马路,必须礼让行人,违反者将被处以
条规定:所有主干道路凡机动车途经十字口或斑马线,无论转弯或者直行,遇有行人过马路,必须礼让行人,违反者将被处以![]() 元罚款,记
元罚款,记![]() 分的行政处罚.如表是本市一主干路段监控设备所抓拍的
分的行政处罚.如表是本市一主干路段监控设备所抓拍的![]() 个月内,机动车驾驶员不“礼让斑马线”行为统计数据:
个月内,机动车驾驶员不“礼让斑马线”行为统计数据:
月份 |
|
|
|
|
|
违章驾驶员人数 |
|
|
|
|
|
(Ⅰ)请利用所给数据求违章人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(Ⅱ)预测该路段![]() 月份的不“礼让斑马线”违章驾驶员人数.
月份的不“礼让斑马线”违章驾驶员人数.
参考公式: ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
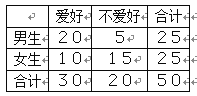
【题目】通过随机询问50名性别不同的大学生是否爱好某项运动,得到如下的列联表,由![]() 得
得![]()
参照附表,得到的正确结论是

A. 有99.5%以上的把握认为“爱好该项运动与性别有关”
B. 有99.5%以上的把握认为“爱好该项运动与性别无关”
C. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥S-ABCD中,![]() 平面
平面![]() ,底面ABCD为直角梯形,
,底面ABCD为直角梯形,![]() ,
,![]() ,且
,且![]()
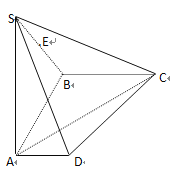
(Ⅰ)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(Ⅱ)若E为SB的中点,在平面![]() 内存在点N,使得
内存在点N,使得![]() 平面
平面![]() ,求N到直线AD,SA的距离.
,求N到直线AD,SA的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com