(1)若A∩B的子集个数为4，求a的范围；

(2)若a∈Z，当A∩B≠时，求a的最小值，并求当a取最小值时A∪B.

A. B. C. D.

【题目】二次函数的图象顶点为，且图象在轴上截得的线段长为8.

（1）求函数的解析式；

（2）令.

（ⅰ）求函数在上的最小值；

（ⅱ）若时，不等式恒成立，试求实数的取值范围.

【题目】已知直线的方程为，其中.

(1)求证：直线恒过定点；

(2)当变化时，求点到直线的距离的最大值；

(3)若直线分别与轴、轴的负半轴交于两点，求面积的最小值及此时直线的方程.

【题目】中国古代儒家要求学生掌握六种基本才艺：礼、乐、射、御、书、数，简称“六艺”,某高中学校为弘扬“六艺”的传统文化，分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识竞赛，现有甲、乙、丙三位选手进入了前三名的最后角逐,规定：每场知识竞赛前三名的得分都分别为且；选手最后得分为各场得分之和，在六场比赛后，已知甲最后得分为分，乙和丙最后得分都是分，且乙在其中一场比赛中获得第一名，下列说法正确的是( )

A. 乙有四场比赛获得第三名

B. 每场比赛第一名得分为

C. 甲可能有一场比赛获得第二名

D. 丙可能有一场比赛获得第一名

【题目】如图：某快递小哥从地出发，沿小路以平均时速20公里小时，送快件到处，已知（公里），，是等腰三角形，．

（1） 试问，快递小哥能否在50分钟内将快件送到处？

（2）快递小哥出发15分钟后，快递公司发现快件有重大问题，由于通讯不畅，公司只能派车沿大路追赶，若汽车平均时速60公里小时，问，汽车能否先到达处？

【题目】近年来随着我国在教育科研上的投入不断加大,科学技术得到迅猛发展,国内企业的国际竞争力得到大幅提升.伴随着国内市场增速放缓,国内有实力企业纷纷进行海外布局,第二轮企业出海潮到来.如在智能手机行业,国产品牌已在赶超国外巨头,某品牌手机公司一直默默拓展海外市场,在海外共设多个分支机构,需要国内公司外派大量后、后中青年员工.该企业为了解这两个年龄层员工是否愿意被外派工作的态度,按分层抽样的方式从后和后的员工中随机调查了位,得到数据如下表：

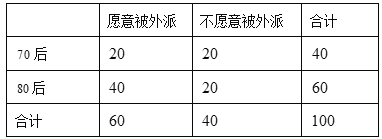
(1)根据调查的数据,是否有以上的把握认为“是否愿意被外派与年龄有关”,并说明理由；

(2)该公司举行参观驻海外分支机构的交流体验活动,拟安排名参与调查的后、后员工参加.后员工中有愿意被外派的人和不愿意被外派的人报名参加,从中随机选出人,记选到愿意被外派的人数为；后员工中有愿意被外派的人和不愿意被外派的人报名参加,从中随机选出人,记选到愿意被外派的人数为,求的概率．

参考数据：

（参考公式：,其中）.

【题目】若是互不相同的空间直线，是不重合的平面，则下列命题中为真命题的是（ ）

A. 若，则 B. 若，则

C. 若，则 D. 若，则

【题目】如图，在长方体中，，点为的中点．

（1）求证：直线平面；

（2）求证：平面平面；

（3）求直线与平面的夹角．

【题目】中国高铁的快速发展给群众出行带来巨大便利，极大促进了区域经济社会发展.已知某条高铁线路通车后，发车时间间隔（单位：分钟）满足，经测算，高铁的载客量与发车时间间隔相关：当时高铁为满载状态，载客量为人；当时，载客量会在满载基础上减少，减少的人数与成正比，且发车时间间隔为分钟时的载客量为人.记发车间隔为分钟时，高铁载客量为.

求的表达式；

若该线路发车时间间隔为分钟时的净收益（元），当发车时间间隔为多少时，单位时间的净收益最大？