
科目: 来源: 题型:
【题目】为响应绿色出行,某市在推出“共享单车”后,又推出“新能源分时租赁汽车”.其中一款新能源分时租赁汽车,每次租车收费的标准由两部分组成:①根据行驶里程数按1元/公里计费;②行驶时间不超过![]() 分时,按
分时,按![]() 元/分计费;超过
元/分计费;超过![]() 分时,超出部分按
分时,超出部分按![]() 元/分计费.已知王先生家离上班地点15公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间
元/分计费.已知王先生家离上班地点15公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间![]() (分)是一个随机变量.现统计了50次路上开车花费时间,在各时间段内的频数分布情况如下表所示:
(分)是一个随机变量.现统计了50次路上开车花费时间,在各时间段内的频数分布情况如下表所示:
时间 |
|
|
|
|
频数 | 2 | 18 | 20 | 10 |
将各时间段发生的频率视为概率,每次路上开车花费的时间视为用车时间,范围为![]() 分.
分.
(1)写出王先生一次租车费用![]() (元)与用车时间
(元)与用车时间![]() (分)的函数关系式;
(分)的函数关系式;
(2)若王先生一次开车时间不超过40分为“路段畅通”,设![]() 表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求
表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求![]() 的分布列和期望;
的分布列和期望;
(3)若公司每月给1000元的车补,请估计王先生每月(按22天计算)的车补是否足够上、下班租用新能源分时租赁汽车?并说明理由.(同一时段,用该区间的中点值作代表)
查看答案和解析>>
科目: 来源: 题型:
【题目】设有三个乡镇,分别位于一个矩形![]() 的两个顶点M,N及
的两个顶点M,N及![]() 的中点S处,
的中点S处,![]() ,现要在该矩形的区域内(含边界),且与M,N等距离的一点O处设一个宣讲站,记O点到三个乡镇的距离之和为
,现要在该矩形的区域内(含边界),且与M,N等距离的一点O处设一个宣讲站,记O点到三个乡镇的距离之和为![]() .
.
(1)设![]() ,试将L表示为x的函数并写出其定义域;
,试将L表示为x的函数并写出其定义域;
(2)试利用(1)的函数关系式确定宣讲站O的位置,使宣讲站O到三个乡镇的距离之和![]() 最小.
最小.
查看答案和解析>>
科目: 来源: 题型:
【题目】f(x)是定义在(0,+∞)上的单调增函数,满足f(xy)=f(x)+f(y),f(3)=1,当f(x)+f(x-8)≤2时,x的取值范围是( )
A.(8,+∞)B.(8,9]C.[8,9]D.(0,8)
查看答案和解析>>
科目: 来源: 题型:
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
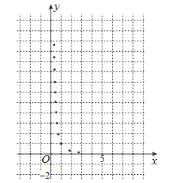
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若旋转的弧度数![]() 与单位时间内煤气输出量
与单位时间内煤气输出量![]() 成正比,那么
成正比,那么![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为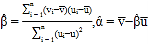 .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 中,角
中,角![]() 、
、![]() 、
、![]() 所对的边分别是
所对的边分别是![]() 、
、![]() 、
、![]() ,且
,且![]() ,
,![]() ,有以下四个命题:①满足条件的
,有以下四个命题:①满足条件的![]() 不可能是直角三角形;②当
不可能是直角三角形;②当![]() 时,
时,![]() 的周长为15;③当
的周长为15;③当![]()
时,若![]() 为
为![]() 的内心,则
的内心,则![]() 的面积为
的面积为![]() ;④
;④ ![]() 的面积的最大值为40.其中正确命题有__________(填写出所有正确命题的序号).
的面积的最大值为40.其中正确命题有__________(填写出所有正确命题的序号).
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (
(![]() 为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,点
为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,点![]() 在直线l:
在直线l:![]() 上.
上.
(1)求曲线C和直线l的直角坐标方程;
(2)若直线l与曲线C的相交于点A、B,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 经过
经过![]() 焦点,且与
焦点,且与![]() 交于
交于![]() 两点满足
两点满足![]() .
.

(1)求抛物线![]() 的方程;
的方程;
(2)已知线段![]() 的垂直平分线与抛物线
的垂直平分线与抛物线![]() 交于
交于![]() 两点,
两点, ![]() 为线段
为线段![]() 的中点,记点
的中点,记点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com