
【题目】为响应绿色出行,某市在推出“共享单车”后,又推出“新能源分时租赁汽车”.其中一款新能源分时租赁汽车,每次租车收费的标准由两部分组成:①根据行驶里程数按1元/公里计费;②行驶时间不超过![]() 分时,按
分时,按![]() 元/分计费;超过
元/分计费;超过![]() 分时,超出部分按
分时,超出部分按![]() 元/分计费.已知王先生家离上班地点15公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间
元/分计费.已知王先生家离上班地点15公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间![]() (分)是一个随机变量.现统计了50次路上开车花费时间,在各时间段内的频数分布情况如下表所示:
(分)是一个随机变量.现统计了50次路上开车花费时间,在各时间段内的频数分布情况如下表所示:
时间 |
|
|
|
|
频数 | 2 | 18 | 20 | 10 |
将各时间段发生的频率视为概率,每次路上开车花费的时间视为用车时间,范围为![]() 分.
分.
(1)写出王先生一次租车费用![]() (元)与用车时间
(元)与用车时间![]() (分)的函数关系式;
(分)的函数关系式;
(2)若王先生一次开车时间不超过40分为“路段畅通”,设![]() 表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求
表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求![]() 的分布列和期望;
的分布列和期望;
(3)若公司每月给1000元的车补,请估计王先生每月(按22天计算)的车补是否足够上、下班租用新能源分时租赁汽车?并说明理由.(同一时段,用该区间的中点值作代表)
科目:高中数学 来源: 题型:
【题目】下列说法:①对于独立性检验,![]() 的值越大,说明两事件相关程度越大;②以模型
的值越大,说明两事件相关程度越大;②以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() ,
,![]() 的值分别是
的值分别是![]() 和
和![]() ;③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程
;③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() ;④通过回归直线
;④通过回归直线![]() 及回归系数
及回归系数![]() ,可以精确反映变量的取值和变化趋势,其中正确的个数是( )
,可以精确反映变量的取值和变化趋势,其中正确的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某单位甲、乙、丙三个部门共有员工60人,为调查他们的睡眠情况,通过分层抽样获得部分员工每天睡眠的时间,数据如下表(单位:小时)
甲部门 | 6 | 7 | 8 | |||
乙部门 | 5.5 | 6 | 6.5 | 7 | 7.5 | 8 |
丙部门 | 5 | 5.5 | 6 | 6.5 | 7 | 8.5 |
(1)求该单位乙部门的员工人数?
(2)从甲部门和乙部门抽出的员工中,各随机选取一人,甲部门选出的员工记为A,乙部门选出的员工记为B,假设所有员工睡眠的时间相互独立,求A的睡眠时间不少于B的睡眠时间的概率;
(3)若将每天睡眠时间不少于7小时视为睡眠充足,现从丙部门抽出的员工中随机抽取3人做进一步的身体检查.用X表示抽取的3人中睡眠充足的员工人数,求随机变量X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,底面ABC为正三角形,
中,底面ABC为正三角形,![]() 底面ABC,
底面ABC,![]() ,点
,点![]() 在线段
在线段![]() 上,平面
上,平面![]() 平面
平面![]() .
.

(1)请指出点![]() 的位置,并给出证明;
的位置,并给出证明;
(2)若![]() ,求
,求![]() 与平面ABE夹角的正弦值.
与平面ABE夹角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 中,角
中,角![]() 、
、![]() 、
、![]() 所对的边分别是
所对的边分别是![]() 、
、![]() 、
、![]() ,且
,且![]() ,
,![]() ,有以下四个命题:①满足条件的
,有以下四个命题:①满足条件的![]() 不可能是直角三角形;②当
不可能是直角三角形;②当![]() 时,
时,![]() 的周长为15;③当
的周长为15;③当![]()
时,若![]() 为
为![]() 的内心,则
的内心,则![]() 的面积为
的面积为![]() ;④
;④ ![]() 的面积的最大值为40.其中正确命题有__________(填写出所有正确命题的序号).
的面积的最大值为40.其中正确命题有__________(填写出所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (
(![]() 为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,点
为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,点![]() 在直线l:
在直线l:![]() 上.
上.
(1)求曲线C和直线l的直角坐标方程;
(2)若直线l与曲线C的相交于点A、B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校组织由5名学生参加的演讲比赛,采用抽签法决定演讲顺序,在“学生![]() 和
和![]() 都不是第一个出场,
都不是第一个出场,![]() 不是最后一个出场”的前提下,学生
不是最后一个出场”的前提下,学生![]() 第一个出场的概率为( )
第一个出场的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 在椭圆
在椭圆![]() :
:![]() 上.若点
上.若点![]() ,
,![]() ,且
,且![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)设椭圆![]() 的焦距为4,
的焦距为4,![]() ,
,![]() 是椭圆
是椭圆![]() 上不同的两点,线段
上不同的两点,线段![]() 的垂直平分线为直线
的垂直平分线为直线![]() ,且直线
,且直线![]() 不与
不与![]() 轴重合.
轴重合.
①若点![]() ,直线
,直线![]() 过点
过点![]() ,求直线
,求直线![]() 的方程;
的方程;
② 若直线![]() 过点
过点![]() ,且与
,且与![]() 轴的交点为
轴的交点为![]() ,求
,求![]() 点横坐标的取值范围.
点横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
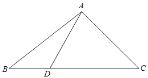
【题目】如图所示,在△ABC中,D是BC边上的一点,且AB=14,BD=6,∠ADC=![]() ,
,![]() .
.
(Ⅰ)求sin∠DAC;
(Ⅱ)求AD的长和△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com