
科目: 来源: 题型:
【题目】一个口袋里装有![]() 个白球和
个白球和![]() 个红球,从口袋中任取
个红球,从口袋中任取![]() 个球.
个球.
(1)共有多少种不同的取法?
(2)其中恰有一个红球,共有多少种不同的取法?
(3)其中不含红球,共有多少种不同的取法?
查看答案和解析>>
科目: 来源: 题型:
【题目】对定义在[0,1]上,并且同时满足以下两个条件的函数f(x)称为G函数.
①对任意的x∈[0,1],总有f(x)≥0;
②当x1≥0,x2≥0,x1+x2≤1时,总有f(x1+x2)≥f(x1)+f(x2)成立.已知函数g(x)=x2与h(x)=2x﹣b是定义在[0,1]上的函数.
(1)试问函数g(x)是否为G函数?并说明理由;
(2)若函数h(x)是G函数,求实数b组成的集合.
查看答案和解析>>
科目: 来源: 题型:
【题目】函数y=f(x)的导函数y=f′(x)的图象如图所示,给出下列命题:
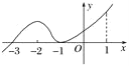
①-3是函数y=f(x)的极值点;
②-1是函数y=f(x)的最小值点;
③y=f(x)在区间(-3,1)上单调递增;
④y=f(x)在x=0处切线的斜率小于零.
以上正确命题的序号是( )
A. ①②B. ③④C. ①③D. ②④
查看答案和解析>>
科目: 来源: 题型:
【题目】某地区2008年至2016年粮食产量的部分数据如下表:

(1)求该地区2008年至2016年的粮食年产量![]() 与年份
与年份![]() 之间的线性回归方程;
之间的线性回归方程;
(2)利用(1)中的回归方程,分析2008年至2016年该地区粮食产量的变化情况,并预测该地区 2018年的粮食产量.
附:回归直线的斜率和截距的最小二乘估计公式分别为 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了响应全民健身,加大国际体育文化的交流,兰州市从2011年开始举办“兰州国际马拉松赛”,为了了解市民健身情况,某课题组跟踪了兰州某跑吧群在各届全程马拉松比赛中群友的平均成绩(单位:小时),具体如下:

(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)的回归方程,分析2011年到2015年该跑吧群的成绩变化情况,反映市民健身的效果,并预测2016年该跑吧群的比赛平均成绩.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在极坐标系中,已知曲线![]() :
:![]() 和曲线
和曲线![]() :
:![]() ,以极点
,以极点![]() 为坐标原点,极轴为
为坐标原点,极轴为![]() 轴非负半轴建立平面直角坐标系.
轴非负半轴建立平面直角坐标系.
(1)求曲线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 是曲线
是曲线![]() 上一动点,过点
上一动点,过点![]() 作线段
作线段![]() 的垂线交曲线
的垂线交曲线![]() 于点
于点![]() ,求线段
,求线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目: 来源: 题型:
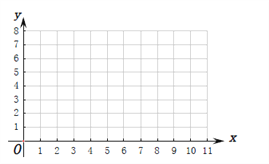
【题目】某商店为了更好地规划某种商品进货的量,该商店从某一年的销售数据中,随机抽取了![]() 组数据作为研究对象,如下图所示(
组数据作为研究对象,如下图所示(![]() (吨)为该商品进货量,
(吨)为该商品进货量, ![]() (天)为销售天数):
(天)为销售天数):
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(Ⅰ)根据上表数据在下列网格中绘制散点图;
(Ⅱ)根据上表提供的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)在该商品进货量![]() (吨)不超过6(吨)的前提下任取两个值,求该商品进货量
(吨)不超过6(吨)的前提下任取两个值,求该商品进货量![]() (吨)恰有一个值不超过3(吨)的概率.
(吨)恰有一个值不超过3(吨)的概率.
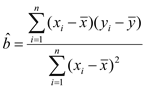 ,
,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com