
科目: 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() 过
过![]() 作圆
作圆![]() 的切线,切点为
的切线,切点为![]() (
(![]() 在第二象限).
在第二象限).
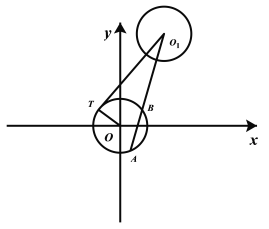
(1)求![]() 的正弦值;
的正弦值;
(2)已知点![]() ,过
,过![]() 点分别作两圆切线,若切线长相等,求
点分别作两圆切线,若切线长相等,求![]() 关系;
关系;
(3)是否存在定点![]() ,使过点
,使过点![]() 有无数对相互垂直的直线
有无数对相互垂直的直线![]() 满足
满足![]() ,且它们分别被圆
,且它们分别被圆![]() 、圆
、圆![]() 所截得的弦长相等?若存在,求出所有的点
所截得的弦长相等?若存在,求出所有的点![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】设点![]() 为椭圆
为椭圆![]() 的左焦点,直线
的左焦点,直线![]() 被椭圆
被椭圆![]() 截得弦长为
截得弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)圆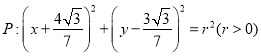 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点, ![]() 为线段
为线段![]() 上任意一点,直线
上任意一点,直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点
两点![]() 为圆
为圆![]() 的直径,且直线
的直径,且直线![]() 的斜率大于
的斜率大于![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 年
年![]() 月某城市国际马拉松赛正式举行,组委会对
月某城市国际马拉松赛正式举行,组委会对![]() 名裁判人员进行业务培训,现按年龄(单位:岁)进行分组统计:第
名裁判人员进行业务培训,现按年龄(单位:岁)进行分组统计:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如下:
,得到的频率分布直方图如下:
(1)培训前组委会用分层抽样调查方式在第![]() 组共抽取了
组共抽取了![]() 名裁判人员进行座谈,若将其中抽取的第
名裁判人员进行座谈,若将其中抽取的第![]() 组的人员记作
组的人员记作![]() ,第
,第![]() 组的人员记作
组的人员记作![]() ,第
,第![]() 组的人员记作
组的人员记作![]() ,若组委会决定从上述
,若组委会决定从上述![]() 名裁判人员中再随机选
名裁判人员中再随机选![]() 人参加新闻发布会,要求这
人参加新闻发布会,要求这![]() 组各选
组各选![]() 人,试求裁判人员
人,试求裁判人员![]() 不同时被选择的概率;
不同时被选择的概率;
(2)培训最后环节,组委会决定从这![]() 名裁判中年龄在
名裁判中年龄在![]() 的裁判人员里面随机选取
的裁判人员里面随机选取![]() 名参加业务考试,设年龄在
名参加业务考试,设年龄在![]() 中选取的人数为
中选取的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形![]() 与梯形
与梯形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() ,
,![]() ∥
∥![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上.
上.

(I)当点![]() 为
为![]() 中点时,求证:
中点时,求证:![]() ∥平面
∥平面![]() ;
;
(II)当平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥PABC中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.

(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求直线AN与平面PMN所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的焦距为2,过短轴的一个端点与两个焦点的圆的面积为
的焦距为2,过短轴的一个端点与两个焦点的圆的面积为![]() ,过椭圆
,过椭圆![]() 的右焦点作斜率为
的右焦点作斜率为![]() (
(![]() )的直线
)的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 垂直于
垂直于![]() 的直线与
的直线与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() .
.
(1)求证:对![]() ,直线
,直线![]() 与圆
与圆![]() 总有两个交点;
总有两个交点;
(2)设直线![]() 与圆
与圆![]() 交于点
交于点![]() ,若
,若![]() ,直线
,直线![]() 的倾斜角;
的倾斜角;
(3)设直线![]() 与圆
与圆![]() 交于点
交于点![]() ,若定点
,若定点![]() 满足
满足![]() ,求此时直线
,求此时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com