【题目】从2017年1月18日开始，支付宝用户可以通过“扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡（爱国福、富强福、和谐福、友善福、敬业福），除夕夜22:18，每一位提前集齐五福的用户都将获得一份现金红包.某高校一个社团在年后开学后随机调查了80位该校在读大学生，就除夕夜22:18之前是否集齐五福进行了一次调查（若未参与集五福的活动，则也等同于未集齐五福），得到具体数据如下表：

（1）根据如上的列联表，能否在犯错误的概率不超过0.05的前提下，认为“集齐五福与性别有关”？

（2）计算这80位大学生集齐五福的频率，并据此估算该校10000名在读大学生中集齐五福的人数；

（3）为了解集齐五福的大学生明年是否愿意继续参加集五福活动，该大学的学生会从集齐五福的学生中，选取2位男生和3位女生逐个进行采访，最后再随机选取3次采访记录放到该大学的官方网站上，求最后被选取的3次采访对象中至少有一位男生的概率.

参考公式： .

附表：

【题目】已知函数.

（1）证明：函数在区间上是减函数；

（2）当时，证明：函数只有一个零点.

在直角坐标系中，直线的参数方程为（为参数）.以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.

（1）若时，求与的交点坐标；

（2）若上的点到距离的最大值为，求.

【题目】已知椭圆的离心率为，，分别为椭圆的左、右焦点，且.

（1）求椭圆的方程；

（2）设为椭圆上任意一点，以为圆心，为半径作圆，当圆与直线：有公共点时，求面积的最大值.

【题目】已知函数（其中），且曲线在点处的切线垂直于直线.

（1）求的值及此时的切线方程；

（2）求函数的单调区间与极值.

【题目】对于集合和常数，定义：为集合相对的“余弦方差”.

（1）若集合，，求集合相对的“余弦方差”；

（2）求证：集合相对任何常数的“余弦方差”是一个与无关的定值，并求此定值；

（3）若集合，，，相对任何常数的“余弦方差”是一个与无关的定值，求出、.

【题目】从某食品厂生产的面包中抽取个，测量这些面包的一项质量指标值，由测量结果得如下频数分布表：

（1）在相应位置上作出这些数据的频率分布直方图；

（2）估计这种面包质量指标值的平均数（同一组中的数据用该组区间的中点值作代表）；

（3）根据以上抽样调查数据，能否认为该食品厂生产的这种面包符合“质量指标值不低于的面包至少要占全部面包的规定？”

【题目】设函数．

（1）当时，求的极值；

（2）当时，证明：．

【题目】对于数列，若存在常数M，使得对任意，与中至少有一个不小于M，则记作，那么下列命题正确的是（ ）．

A.若，则数列各项均大于或等于M；

B.若，则；

C.若，，则；

D.若，则；

该兴趣小组确定的研究方案是：先从这六组数据中选取2组，用剩下的4组数据求线性回归方程，再用被选取的2组数据进行检验。

(Ⅰ)求选取的2组数据恰好是相邻两个星期的概率；

(Ⅱ)若选取的是第一周与第六周的两组数据，请根据第二周到第五周的4组数据,求出关于的线性回归方程；

(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?

(参考公式: )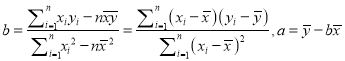

参考数据： 1092， 498