A. B. C. D.

（1）写出图（1）表示的市场售价与时间的函数关系式写出图（2）表示的种植成本与时间的函数关系式

（2）认定市场售价减去种植成本为纯收益，问何时上市的西红柿收益最大？（注：市场售价和种植成本的单位：元/kg，时间单位：天.）

【题目】已知等腰梯形ABCD(如图1所示)，其中AB∥CD，E，F分别为AB和CD的中点，且AB＝EF＝2，CD＝6，M为BC中点．现将梯形ABCD沿着EF所在直线折起，使平面EFCB⊥平面EFDA(如图2所示)，N是线段CD上一动点，且.

(1)求证：MN∥平面EFDA；

(2)求三棱锥A－MNF的体积．

【题目】若函数同时满足：(1)对于定义域上的任意，恒有；(2)对于定义域上的任意，，当时，恒有，则称函数为“理想函数”．给出下列四个函数中：①； ②； ③；④，则被称为“理想数”的有________(填相应的序号)．

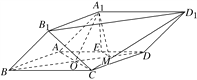
(1)证明：A1O∥平面B1CD1；

(2)设M是OD的中点，证明：平面A1EM⊥平面B1CD1.

【题目】如图，已知多面体的底面是边长为2的菱形且，平面，，.

（1）证明：平面平面；

（2）求二面角的余弦值.

【题目】某农业合作社生产了一种绿色蔬菜共吨，如果在市场上直接销售，每吨可获利万元；如果进行精加工后销售，每吨可获利万元，但需另外支付一定的加工费，总的加工（万元）与精加工的蔬菜量（吨）有如下关系：设该农业合作社将（吨）蔬菜进行精加工后销售，其余在市场上直接销售，所得总利润（扣除加工费）为（万元）．

（1）写出关于的函数表达式；

（2）当精加工蔬菜多少吨时，总利润最大，并求出最大利润．

(1)求证：平面PAB⊥平面QBC；

(2)求该组合体QPABCD的体积．

【题目】如图所示，在四棱锥P－ABCD中，PA⊥底面ABCD，PA＝2，∠ABC＝90°，，BC＝1， ，∠ACD＝60°，E为CD的中点．

(1)求证：BC∥平面PAE；

(2)求点A到平面PCD的距离．