
科目: 来源: 题型:
【题目】在某次高中学科知识竞赛中,对4000名考生的参赛成绩进行统计,可得到如图所示的频率分布直方图,其中分组的区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,60分以下视为不及格,若同一组中数据用该组区间中间值作代表值,则下列说法中正确的是( )
,60分以下视为不及格,若同一组中数据用该组区间中间值作代表值,则下列说法中正确的是( )
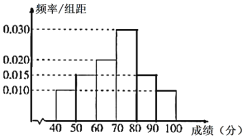
A.成绩在![]() 的考生人数最多B.不及格的考生人数为1000
的考生人数最多B.不及格的考生人数为1000
C.考生竞赛成绩的平均分约为70D.考生竞赛成绩的中位数为75分
查看答案和解析>>
科目: 来源: 题型:
【题目】设抛物线C:y2=4x焦点为F,直线l与C交于A,B两点.
(1)若l过F且斜率为1,求|AB|;
(2)若不过坐标原点O,且OA⊥OB,证明:直线l过定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着节能减排意识深入人心以及共享单车在饶城的大范围推广,越来越多的市民在出行时喜欢选择骑行共享单车。为了研究广大市民在共享单车上的使用情况,某公司在我市随机抽取了100名用户进行调查,得到如下数据:
每周使用次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 4 | 3 | 3 | 7 | 8 | 30 |
女 | 6 | 5 | 4 | 4 | 6 | 20 |
合计 | 10 | 8 | 7 | 11 | 14 | 50 |
(1)如果认为每周使用超过3次的用户为“喜欢骑行共享单车”,请完成![]() 列表(见答题卡),并判断能否在犯错误概率不超过0.05的前提下,认为是否“喜欢骑行共享单车”与性别有关?
列表(见答题卡),并判断能否在犯错误概率不超过0.05的前提下,认为是否“喜欢骑行共享单车”与性别有关?
(2)每周骑行共享单车6次及6次以上的用户称为“骑行达人”,视频率为概率,在我市所有“骑行达人”中,随机抽取4名用户.
① 求抽取的4名用户中,既有男生“骑行达人”又有女“骑行达人”的概率;
②为了鼓励女性用户使用共享单车,对抽出的女“骑行达人”每人奖励500元,记奖励总金额为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表及公式: 
0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |
2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]()
![]() 为偶函数,且函数
为偶函数,且函数![]() 的图象的两相邻对称轴间的距离为
的图象的两相邻对称轴间的距离为![]() .
.
(1)求![]() 的值;
的值;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度后,再将得到的图象上各点的横坐标伸长为原来的4倍,纵坐标不变,得到函数
个单位长度后,再将得到的图象上各点的横坐标伸长为原来的4倍,纵坐标不变,得到函数![]() 的图象,求函数
的图象,求函数![]() 的单调递减区间.
的单调递减区间.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面四个命题:
①![]() 在定义域上单调递增;
在定义域上单调递增;
②若锐角![]() ,
,![]() 满足
满足![]() ,则
,则![]() ;
;
③![]() 是定义在
是定义在![]() 上的偶函数,且在
上的偶函数,且在![]() 上是增函数,若
上是增函数,若![]() ,则
,则![]() ;
;
④函数![]() 的一个对称中心是
的一个对称中心是![]() ;
;
其中真命题的序号为______.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,且直线
,且直线![]() 是其图象的一条对称轴.
是其图象的一条对称轴.
(1)求函数![]() 的解析式;
的解析式;
(2)在![]() 中,角
中,角![]() 、
、![]() 、
、![]() 所对的边分别为
所对的边分别为![]() 、
、![]() 、
、![]() ,且
,且![]() ,
,![]() ,若
,若![]() 角满足
角满足![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的
个单位,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的![]() 倍后所得到的图象对应的函数记作
倍后所得到的图象对应的函数记作![]() ,已知常数
,已知常数![]() ,
,![]() ,且函数
,且函数![]() 在
在![]() 内恰有
内恰有![]() 个零点,求常数
个零点,求常数![]() 与
与![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】钓鱼岛及其附属岛屿是中国固有领土,如图:点A、B、C分别表示钓鱼岛、南小岛、黄尾屿,点C在点A的北偏东47°方向,点B在点C的南偏西36°方向,点B在点A的南偏东79°方向,且A、B两点的距离约为3海里.

(1)求A、C两点间的距离;(精确到0.01)
(2)某一时刻,我国一渔船在A点处因故障抛锚发出求救信号.一艘R国舰艇正从点C正东10海里的点P处以18海里/小时的速度接近渔船,其航线为P![]() C
C![]() A(直线行进),而我东海某渔政船正位于点A南偏西60°方向20海里的点Q处,收到信号后赶往救助,其航线为先向正北航行8海里至点M处,再折向点A直线航行,航速为22海里/小时.渔政船能否先于R国舰艇赶到进行救助?说明理由.
A(直线行进),而我东海某渔政船正位于点A南偏西60°方向20海里的点Q处,收到信号后赶往救助,其航线为先向正北航行8海里至点M处,再折向点A直线航行,航速为22海里/小时.渔政船能否先于R国舰艇赶到进行救助?说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 的两条相邻对称轴之间的距离为
的两条相邻对称轴之间的距离为![]() .
.
(1)求![]() 的值;
的值;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再将所得函数的图象上所有点的横坐标伸长到原来的2倍,纵坐标不变,得到函数
个单位,再将所得函数的图象上所有点的横坐标伸长到原来的2倍,纵坐标不变,得到函数![]() 的图象,若函数
的图象,若函数![]() 在区间
在区间![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com