
科目: 来源: 题型:
【题目】已知一元二次函数![]() 的图像与
的图像与![]() 轴有两个不同的交点,其中一个交点的坐标为
轴有两个不同的交点,其中一个交点的坐标为![]() 且当
且当![]() 时,恒有
时,恒有![]()
(1)求出不等式![]() 的解(用
的解(用![]() 表示);
表示);
(2)若以二次函数的图像与坐标轴的三个交点为顶点的三角形的面积为8,求![]() 的取值范围;
的取值范围;
(3)若不等式![]() 对所有
对所有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知倾斜角为![]() 的直线经过抛物线
的直线经过抛物线![]() :
:![]() 的焦点
的焦点![]() ,与抛物线
,与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)过点![]() 的两条直线
的两条直线![]() 、
、![]() 分别交抛物线
分别交抛物线![]() 于点
于点![]() 、
、![]() 和
和![]() 、
、![]() ,线段
,线段![]() 和
和![]() 的中点分别为
的中点分别为![]() 、
、![]() .如果直线
.如果直线![]() 与
与![]() 的倾斜角互余,求证:直线
的倾斜角互余,求证:直线![]() 经过一定点.
经过一定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
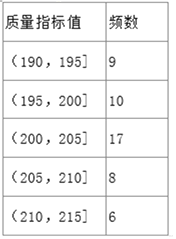
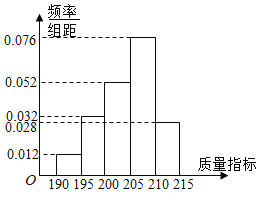
(1)根据频率分布直方图,估计乙流水线生产的产品该质量指标值的中位数;
(2)若将频率视为概率,某个月内甲、乙两条流水线均生产了5000件产品,则甲、乙两条流水线分别生产出不合格品约多少件?
(3)根据已知条件完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
甲流水线 | 乙流水线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:![]() ,其中
,其中![]() .
.
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】在物理学中,声波在单位时间内作用在与其传递方向垂直的单位面积上的能量称声强.日常生活中能听到的声音其声强范围很大,最大和最小之间的比值可达![]() 倍.用声强的物理学单位表示声音强弱很不方便。当人耳听到两个强度不同的声音时,感觉的大小大致上与两个声强比值的常用对数成比例.所以引入声强级来表示声音的强弱.
倍.用声强的物理学单位表示声音强弱很不方便。当人耳听到两个强度不同的声音时,感觉的大小大致上与两个声强比值的常用对数成比例.所以引入声强级来表示声音的强弱.
某一处的声强级,是指该处的声强P与参考声强![]() 的比值的常用对数,单位为贝尔(B),其中参考声强
的比值的常用对数,单位为贝尔(B),其中参考声强![]() 瓦/米2实际生活中一般用1贝尔的十分之一,即分贝(
瓦/米2实际生活中一般用1贝尔的十分之一,即分贝(![]() )来作为声强级的单位,其公式为声强级
)来作为声强级的单位,其公式为声强级 .若某工厂环境内有一台机器(声源)单独运转时,发出噪声的声强级为80分贝,那么两台相同的机器一同运转时(声强为原来的两倍),发出噪声的声强级为分______贝(精确到0.1分).
.若某工厂环境内有一台机器(声源)单独运转时,发出噪声的声强级为80分贝,那么两台相同的机器一同运转时(声强为原来的两倍),发出噪声的声强级为分______贝(精确到0.1分).
查看答案和解析>>
科目: 来源: 题型:
【题目】设椭圆![]() 的离心率为
的离心率为![]() ,左顶点到直线
,左顶点到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线![]() 与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点O,试探究:点O到直线AB的距离是否为定值?若是,求出这个定值;否则,请说明理由;
与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点O,试探究:点O到直线AB的距离是否为定值?若是,求出这个定值;否则,请说明理由;
(Ⅲ)在(Ⅱ)的条件下,试求△AOB面积S的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=![]() 若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式。
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
查看答案和解析>>
科目: 来源: 题型:
【题目】如果一个函数![]() 的图像是一个中心对称图形,关于点
的图像是一个中心对称图形,关于点![]() 对称,那么将
对称,那么将![]() 的图像向左平移m个单位再向下平移n的单位后得到一个关于原点对称的函数图像.即函数
的图像向左平移m个单位再向下平移n的单位后得到一个关于原点对称的函数图像.即函数![]() 为奇函数.那么下列命题中真命题的个数是( )
为奇函数.那么下列命题中真命题的个数是( )
①二次函数![]() (
(![]() )的图像肯定不是一个中心对称图形;
)的图像肯定不是一个中心对称图形;
②三次函数![]() (
(![]() )的图像肯定是一个中心对称图形;
)的图像肯定是一个中心对称图形;
③函数![]() (
(![]() 且
且![]() )的图像肯定是一个中心对称图形.
)的图像肯定是一个中心对称图形.
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() 的图像为直线
的图像为直线![]() .
.
(Ⅰ)当![]() 时,若函数
时,若函数![]() 的图像永远在直线
的图像永远在直线![]() 下方,求实数
下方,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)当![]() 时,若直线
时,若直线![]() 与函数
与函数![]() 的图像的有两个不同的交点
的图像的有两个不同的交点![]() ,线段
,线段![]() 的中点为
的中点为![]()
![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com