
【题目】已知一元二次函数![]() 的图像与
的图像与![]() 轴有两个不同的交点,其中一个交点的坐标为
轴有两个不同的交点,其中一个交点的坐标为![]() 且当
且当![]() 时,恒有
时,恒有![]()
(1)求出不等式![]() 的解(用
的解(用![]() 表示);
表示);
(2)若以二次函数的图像与坐标轴的三个交点为顶点的三角形的面积为8,求![]() 的取值范围;
的取值范围;
(3)若不等式![]() 对所有
对所有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用![]() 求得
求得![]() 关于
关于![]() 的表达式,进而求得不等式
的表达式,进而求得不等式![]() 的解集.
的解集.
(2)根据(1)求得三个交点的坐标,利用面积列方程,求得![]() 的表达式,进而求得
的表达式,进而求得![]() 的取值范围.
的取值范围.
(3)根据(1)中求得![]() 的表达式化简不等式
的表达式化简不等式![]() .对
.对![]() 分成
分成![]() 三种情况进行分类讨论,由此求得
三种情况进行分类讨论,由此求得![]() 的取值范围.
的取值范围.
(1)依题意可知![]() ,即
,即![]() ①,由
①,由![]() ,故①式可化为
,故①式可化为![]() .所以
.所以![]()
![]() .令
.令![]() ,解得
,解得![]() ,
,![]() .由于当
.由于当![]() 时,恒有
时,恒有![]() ,所以
,所以![]() .令
.令![]() ,解得
,解得![]() .所以不等式
.所以不等式![]() 的解集为
的解集为![]() .
.
(2)结合(1)可知,三个交点的坐标为![]() ,且
,且![]() .根据三角形的面积得
.根据三角形的面积得![]() ,化简得
,化简得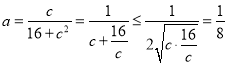 ,
,![]() 时等号成立,故
时等号成立,故![]() 的取值范围是
的取值范围是![]() .
.
(3)由于![]() ,所以不等式
,所以不等式![]() 可化为
可化为![]() ②.
②.
当![]() 时,②成立.
时,②成立.
当![]() 时,②可化为
时,②可化为![]() ,而
,而![]() ,所以
,所以![]() .
.
当![]() 时,②可化为
时,②可化为![]() ,而
,而![]() ,所以
,所以![]() .
.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】椭圆的中心在原点,焦点在坐标轴上,焦距为2![]() .一双曲线和该椭圆有公共焦点,且双曲线的实半轴长比椭圆的长半轴长小4,双曲线离心率与椭圆离心率之比为7∶3,求椭圆和双曲线的方程.
.一双曲线和该椭圆有公共焦点,且双曲线的实半轴长比椭圆的长半轴长小4,双曲线离心率与椭圆离心率之比为7∶3,求椭圆和双曲线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率为
的离心率为![]() ,左顶点到直线
,左顶点到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线![]() 与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点O,试探究:点O到直线AB的距离是否为定值?若是,求出这个定值;否则,请说明理由;
与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点O,试探究:点O到直线AB的距离是否为定值?若是,求出这个定值;否则,请说明理由;
(Ⅲ)在(Ⅱ)的条件下,试求△AOB面积S的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一景区的截面图,![]() 是可以行走的斜坡,已知
是可以行走的斜坡,已知![]() 百米,
百米,![]() 是没有人行路(不能攀登)的斜坡,
是没有人行路(不能攀登)的斜坡,![]() 是斜坡上的一段陡峭的山崖.假设你(看做一点)在斜坡
是斜坡上的一段陡峭的山崖.假设你(看做一点)在斜坡![]() 上,身上只携带着量角器(可以测量以你为顶点的角).
上,身上只携带着量角器(可以测量以你为顶点的角).
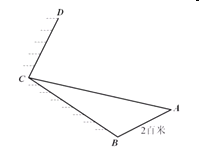
(1)请你设计一个通过测量角可以计算出斜坡![]() 的长的方案,用字母表示所测量的角,计算出
的长的方案,用字母表示所测量的角,计算出![]() 的长,并化简;
的长,并化简;
(2)设![]() 百米,
百米,![]() 百米,
百米,![]() ,
,![]() ,求山崖
,求山崖![]() 的长.(精确到米)
的长.(精确到米)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》卷第五《商功》中有记载:“刍甍者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶.”现有一个刍甍,如图,四边形![]() 为正方形,四边形
为正方形,四边形![]() 、
、![]() 为两个全等的等腰梯形,
为两个全等的等腰梯形,![]() ,
,![]() ,若这个刍甍的体积为
,若这个刍甍的体积为![]() ,则
,则![]() 的长为( )
的长为( )
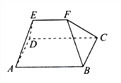
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度![]() (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度![]() (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当![]() 时,
时,![]() 的值为2千克/年;当
的值为2千克/年;当![]() 时,
时,![]() 是
是![]() 的一次函数;当
的一次函数;当![]() 时,因缺氧等原因,
时,因缺氧等原因,![]() 的值为0千克/年.
的值为0千克/年.
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的函数表达式.
的函数表达式.
(2)当养殖密度![]() 为多少时,鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
为多少时,鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为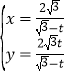 (
(![]() 为参数,且
为参数,且![]() ),以坐标原点为极点,
),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 的参数方程化为普通方程,并将曲线
的参数方程化为普通方程,并将曲线![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求曲线![]() 与曲线
与曲线![]() 交点的极坐标
交点的极坐标![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com