
科目: 来源: 题型:
【题目】如图①,有一个长方体形状的敞口玻璃容器,底面是边长为20cm的正方形,高为30cm,内有20cm深的溶液.现将此容器倾斜一定角度![]() (图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
(图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
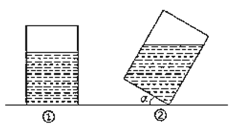
(1)要使倾斜后容器内的溶液不会溢出,角![]() 的最大值是多少?
的最大值是多少?
(2)现需要倒出不少于![]() 的溶液,当
的溶液,当![]() 时,能实现要求吗?请说明理由.
时,能实现要求吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标平面内,以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为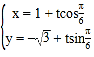 (
(![]() 为参数).
为参数).
(1)分别求出曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 在曲线
在曲线![]() 上,且
上,且![]() 到直线
到直线![]() 的距离为1,求满足这样条件的点
的距离为1,求满足这样条件的点![]() 的个数.
的个数.
查看答案和解析>>
科目: 来源: 题型:
【题目】直角坐标平面内,每个点绕原点按逆时针方向旋转![]() 的变换
的变换![]() 所对应的矩阵为
所对应的矩阵为![]() ,每个点横、纵坐标分别变为原来的
,每个点横、纵坐标分别变为原来的![]() 倍的变换
倍的变换![]() 所对应的矩阵为
所对应的矩阵为![]() .
.
(I)求矩阵![]() 的逆矩阵
的逆矩阵![]() ;
;
(Ⅱ)求曲线![]() 先在变换
先在变换![]() 作用下,然后在变换
作用下,然后在变换![]() 作用下得到的曲线方程.
作用下得到的曲线方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分12分)
如图在直三棱柱ABC—A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的
中点.
(1) 求证: AC⊥BC1
(2) 求证:AC1∥平面CDB1
(3) 求异面直线AC1与B1C所成角的余弦值.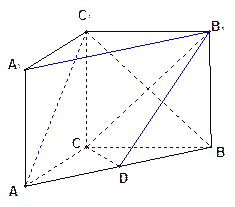
查看答案和解析>>
科目: 来源: 题型:
【题目】某市公园内的人工湖上有一个以点![]() 为圆心的圆形喷泉,沿湖有一条小径
为圆心的圆形喷泉,沿湖有一条小径![]() ,在
,在![]() 的另一侧建有控制台
的另一侧建有控制台![]() ,
,![]() 和
和![]() 之间均有小径连接(小径均为直路),且
之间均有小径连接(小径均为直路),且![]() ,喷泉中心
,喷泉中心![]() 点距离
点距离![]() 点60米,且
点60米,且![]() 连线恰与
连线恰与![]() 平行,在小径
平行,在小径![]() 上有一拍照点
上有一拍照点![]() ,现测得
,现测得![]() 米,
米, ![]() 米,且
米,且![]() .
.
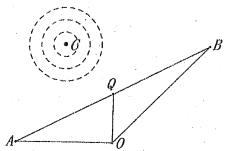
(I)请计算小径![]() 的长度;
的长度;
(Ⅱ)现打算改建控制台![]() 的位置,其离喷泉尽可能近,在点
的位置,其离喷泉尽可能近,在点![]() 的位置及
的位置及![]() 大小均不变的前提下,请计算
大小均不变的前提下,请计算![]() 距离的最小值;
距离的最小值;
(Ⅲ)一人从小径一端![]() 处向
处向![]() 处匀速前进时,喷泉恰好同时开启,喷泉开启
处匀速前进时,喷泉恰好同时开启,喷泉开启![]() 分钟后的水幕是一个以
分钟后的水幕是一个以![]() 为圆心,半径
为圆心,半径![]() 米的圆形区域(含边界),此人的行进速度是
米的圆形区域(含边界),此人的行进速度是![]() 米/分钟,在这个人行进的过程中他会被水幕沾染,试求实数
米/分钟,在这个人行进的过程中他会被水幕沾染,试求实数![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:

(1)若采用样本估计总体的方式,试估计小王的所有微信好友中每日走路步数超过5000步的概率;
(2)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?


查看答案和解析>>
科目: 来源: 题型:
【题目】中国古代名词“刍童”原来是草堆的意思,古代用它作为长方体棱台(上、下底面均为矩形额棱台)的专用术语,关于“刍童”体积计算的描述,《九章算术》注曰:“倍上表,下表从之,亦倍小表,上表从之,各以其广乘之,并,以高若深乘之,皆六面一.”其计算方法是:将上底面的长乘二,与下底面的长相加,再与上底面的宽相乘;将下底面的长乘二,与上底面的长相加,再与下底面的宽相乘;把这两个数值相加,与高相乘,再取其六分之一,以此算法,现有上下底面为相似矩形的棱台,相似比为![]() ,高为3,且上底面的周长为6,则该棱台的体积的最大值是( )
,高为3,且上底面的周长为6,则该棱台的体积的最大值是( )
A. 14 B. 56 C. ![]() D. 63
D. 63
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为 (
(![]() 为参数,
为参数,![]() ),以
),以![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com