
【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:

(1)若采用样本估计总体的方式,试估计小王的所有微信好友中每日走路步数超过5000步的概率;
(2)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】(1)已知四棱锥![]() 的侧棱长与底面边长都相等,四边形
的侧棱长与底面边长都相等,四边形![]() 为正方形,点
为正方形,点![]() 是
是![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.

(2)如图,在长方体![]() 中,
中,![]() 分别是
分别是![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有红、黄、白色球各1个,每次任取1个,有放回地抽三次,求基本事件的个数,写出所有基本事件的全集,并计算下列事件的概率:
(1)三次颜色各不相同;
(2)三次颜色不全相同;
(3)三次取出的球无红色或黄色.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面内,以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为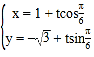 (
(![]() 为参数).
为参数).
(1)分别求出曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 在曲线
在曲线![]() 上,且
上,且![]() 到直线
到直线![]() 的距离为1,求满足这样条件的点
的距离为1,求满足这样条件的点![]() 的个数.
的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的对称轴方程;
的对称轴方程;
(2)将函数![]() 的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移
的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.若
的图象.若![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() △三个内角
△三个内角![]() ,
, ![]() ,
, ![]() 的对边,
的对边, ![]() ,
, ![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园欲将一块空地规划成如图所示的区域,其中在边长为20米的正方形![]() 内种植经红色郁金香,在正方形
内种植经红色郁金香,在正方形![]() 的剩余部分(即四个直角三角形内)种植黄色郁金香.现要在以
的剩余部分(即四个直角三角形内)种植黄色郁金香.现要在以![]() 为边长的矩形
为边长的矩形![]() 内种植绿色草坪,要求绿色草坪的面积等于黄色郁金香的面积.设
内种植绿色草坪,要求绿色草坪的面积等于黄色郁金香的面积.设![]() ,
,![]() 米.
米.

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com