
科目: 来源: 题型:
【题目】经观测,某公路段在某时段内的车流量![]() (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度![]() (千米/小时)之间有函数关系:
(千米/小时)之间有函数关系:![]() .
.
(1)在该时段内,当汽车的平均速度![]() 为多少时车流量
为多少时车流量![]() 最大?最大车流量为多少?(精确到0.01)
最大?最大车流量为多少?(精确到0.01)
(2)为保证在该时段内车流量至少为10千辆/小时,则汽车的平均速度应控制在什么范围内?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求k的值;
(2)设g(x)=log4![]() ,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】为迎接2017年“双![]() ”,“双
”,“双![]() ”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共
”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共![]() 个,生产一个汤碗需
个,生产一个汤碗需![]() 分钟,生产一个花瓶需
分钟,生产一个花瓶需![]() 分钟,生产一个茶杯需
分钟,生产一个茶杯需![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过![]() 小时.若生产一个汤碗可获利润
小时.若生产一个汤碗可获利润![]() 元,生产一个花瓶可获利润
元,生产一个花瓶可获利润![]() 元,生产一个茶杯可获利润
元,生产一个茶杯可获利润![]() 元.
元.
(1)使用每天生产的汤碗个数![]() 与花瓶个数
与花瓶个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需维护费150元,未租出的车每辆每月需要维护费50元。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】电视传媒公司为了解某地区观众对某类休育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
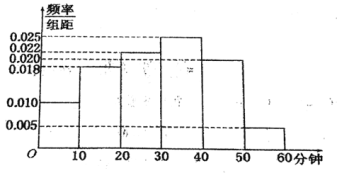
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
(1)根据已知条件完成下面的![]() 列联表,并据此资料判断是否有
列联表,并据此资料判断是否有![]() 的把握认为“体育迷”与性别有关?
的把握认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | |||
合计 |
(2)将日均收看读体育节目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率.
附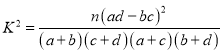 .
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() 的最小正期为
的最小正期为![]() .
.
(1)求![]() 的单调增区间;
的单调增区间;
(2)方程![]() 在
在![]() 上有且只有一个解,求实数
上有且只有一个解,求实数![]() 的取值范围;
的取值范围;
(3)是否存在实数![]() 满足对任意
满足对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立.若存在,求
成立.若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】先阅读下列不等式的证法,再解决后面的问题:
已知![]() ,
,![]() ,求证:
,求证:![]() .
.
证明:构造函数![]() ,
,
即![]()
![]() .
.
因为对一切![]() ,恒有
,恒有![]() ,
,
所以![]() ,从而得
,从而得![]() .
.
(1)若![]() ,
,![]() ,请写出上述结论的推广式;
,请写出上述结论的推广式;
(2)参考上述证法,对你推广的结论加以证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数![]() .
.
(1)若![]() 是
是![]() 的两个不同的根,是否存在实数
的两个不同的根,是否存在实数![]() ,使
,使![]() 成立?若存在,求
成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(2)设![]() ,函数
,函数![]() 已知方程
已知方程![]() 恰有3个不同的根.
恰有3个不同的根.
(ⅰ)求![]() 的取值范围;
的取值范围;
(ⅱ)设![]() 分别是这3个根中的最小值与最大值,求
分别是这3个根中的最小值与最大值,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com