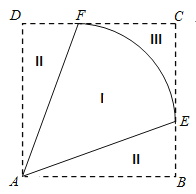
【题目】某地拟规划种植一批芍药，为了美观，将种植区域（区域I）设计成半径为1km的扇形，中心角（）.为方便观赏，增加收入，在种植区域外围规划观赏区（区域II）和休闲区（区域III），并将外围区域按如图所示的方案扩建成正方形，其中点，分别在边和上．已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.

（1）要使观赏区的年收入不低于5万元，求的最大值；

（2）试问：当为多少时，年总收入最大？

【题目】已知函数，其中．

Ⅰ当时，恒成立，求a的取值范围；

Ⅱ设是定义在上的函数，在内任取个数，，，，，设，令，，如果存在一个常数，使得恒成立，则称函数在区间上的具有性质P.试判断函数在区间上是否具有性质P？若具有性质P，请求出M的最小值；若不具有性质P，请说明理由．注：

【题目】药材人工种植技术具有养殖密度高、经济效益好的特点．研究表明：人工种植药材时，某种药材在一定的条件下，每株药材的年平均生长量单位：千克是每平方米种植株数x的函数．当x不超过4时，v的值为2；当时，v是x的一次函数，其中当x为10时，v的值为4；当x为20时，v的值为0．

当时，求函数v关于x的函数表达式；

当每平方米种植株数x为何值时，每平方米药材的年生长总量单位：千克取得最大值？并求出这个最大值．年生长总量年平均生长量种植株数

【题目】已知集合，其中，由中的元素构成两个相应的集合：

， ．

其中是有序数对，集合和中的元素个数分别为和．

若对于任意的，总有，则称集合具有性质．

（Ⅰ）检验集合与是否具有性质并对其中具有性质的集合，写出相应的集合和．

（Ⅱ）对任何具有性质的集合，证明．

（Ⅲ）判断和的大小关系，并证明你的结论．

【题目】已知椭圆，过右焦点的直线与椭圆交于两点，且当点是椭圆的上顶点时，，线段的中点为．

（1）求椭圆的方程；

（2）延长线段与椭圆交于点，若，求此时的方程．

【题目】在直角坐标系xOy中，曲线C1：（α为参数），以O为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ2－4ρcosθ－3＝0，直线l的极坐标方程为θ＝（ρ∈R）．

（Ⅰ）求曲线C1的极坐标方程与直线l的直角坐标方程；

（Ⅱ）若直线l与曲线C1，C2在第一象限分别交于A，B两点，P为曲线C1上的动点，求△PAB面积的最大值．

（Ⅰ）讨论f（x）在[0，＋∞）上的单调性；

（Ⅱ）若函数g（x）＝f（x）＋x有两个极值点x1，x2，且x1＜x2，求证:g（x2）＞－ln2．

【题目】已知四棱锥的底面ABCD是菱形，平面ABCD，，，F，G分别为PD，BC中点，.

（Ⅰ）求证：平面PAB；

（Ⅱ）求三棱锥的体积；

（Ⅲ）求证：OP与AB不垂直.

【题目】已知函数f(x)=,下列结论中错误的是

A. , f()=0

B. 函数y=f(x)的图像是中心对称图形

C. 若是f(x)的极小值点，则f(x)在区间（-∞,）单调递减

D. 若是f（x）的极值点，则()=0

【题目】已知直线l1：y＝x，l2：y＝－x，动点P，Q分别在l1，l2上移动，｜PQ｜＝2，N是线段PQ的中点，记点N的轨迹为曲线C．

（Ⅰ）求曲线C的方程；

（Ⅱ）过点M（0，1）分别作直线MA，MB交曲线C于A，B两点，设这两条直线的斜率分别为k1，k2，且k1＋k2＝2，证明：直线AB过定点．