
科目: 来源: 题型:
【题目】某厂生产的某种零件的尺寸![]() 大致服从正态分布
大致服从正态分布![]() ,且规定尺寸
,且规定尺寸![]() 为次品,其余的为正品.生产线上的打包机自动把每5件零件打包成1箱,然后进入销售环节,若每销售一件正品可获利50元,每销售一件次品亏损100元.现从生产线生产的零件中抽样20箱做质量分析,作出的频率分布直方图如下:
为次品,其余的为正品.生产线上的打包机自动把每5件零件打包成1箱,然后进入销售环节,若每销售一件正品可获利50元,每销售一件次品亏损100元.现从生产线生产的零件中抽样20箱做质量分析,作出的频率分布直方图如下:
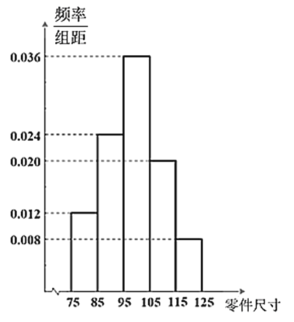
(1)估计生产线生产的零件的次品率及零件的平均尺寸;
(2)从生产线上随机取一箱零件,求这箱零件销售后的期望利润及不亏损的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为 (其中t为参数),现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρ=4sinθ.
(其中t为参数),现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρ=4sinθ.
(Ⅰ)写出直线l和曲线C的普通方程;
(Ⅱ)已知点P为曲线C上的动点,求P到直线l的距离的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某单位为了响应疫情期间有序复工复产的号召,组织从疫区回来的甲、乙、丙、丁4名员工进行核酸检测,现采用抽签法决定检测顺序,在“员工甲不是第一个检测,员工乙不是最后一个检测”的条件下,员工丙第一个检测的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法正确的有( )
①在回归分析中,可以借助散点图判断两个变量是否呈线性相关关系.
②在回归分析中,可以通过残差图发现原始数据中的可疑数据,残差平方和越小,模型的拟合效果越好.
③在回归分析模型中,相关系数的绝对值越大,说明模型的拟合效果越好.
④在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,预报变量
每增加1个单位时,预报变量![]() 增加0.1个单位.
增加0.1个单位.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ex-x2+a,x∈R,曲线y=f(x)在(0,f(0))处的切线方程为y=bx.
(1)求f(x)的解析式;
(2)当x∈R时,求证:f(x)≥-x2+x;
(3)若f(x)≥kx对任意的x∈(0,+∞)恒成立,求实数k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学高二年级组织外出参加学业水平考试,出行方式为:乘坐学校定制公交或自行打车前往,大数据分析显示,当![]() 的学生选择自行打车,自行打车的平均时间为
的学生选择自行打车,自行打车的平均时间为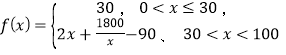 (单位:分钟) ,而乘坐定制公交的平均时间不受
(单位:分钟) ,而乘坐定制公交的平均时间不受![]() 影响,恒为40分钟,试根据上述分析结果回答下列问题:
影响,恒为40分钟,试根据上述分析结果回答下列问题:
(1)当![]() 在什么范围内时,乘坐定制公交的平均时间少于自行打车的平均时间?
在什么范围内时,乘坐定制公交的平均时间少于自行打车的平均时间?
(2)求该校学生参加考试平均时间![]() 的表达式:讨论
的表达式:讨论![]() 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
查看答案和解析>>
科目: 来源: 题型:
【题目】【2018海南高三阶段性测试(二模)】如图,在直三棱柱![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上一动点.
上一动点.

(I)是否存在一点![]() ,使得线段
,使得线段![]() 平面
平面![]() ?若存在,指出点
?若存在,指出点![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
(II)若点![]() 为
为![]() 的中点且
的中点且![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com