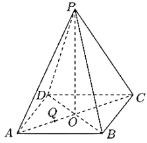
【题目】《九章算术》是我国古代数学名著，它在几何学中的研究比西方早1千多年.在《九章算术》中，将底面为直角三角形，且侧棱垂直于底面的三棱柱称为堑堵，阳马指底面为矩形，一侧棱垂直于底面的四棱锥，鳖臑指四个面均为直角三角形的四面体.如图，在堑堵中，.

（1）求证：四棱锥为阳马；并判断四面体是否为鳖臑，若是，请写出各个面的直角（要求写出结论）.

（2）若，当阳马体积最大时，求二面角的余弦值.

（1）男运动员3名，女运动员2名；

（2）至少有1名女运动员；

（3）队长中至少有1人参加；

（4）既要有队长，又要有女运动员.

【题目】有一段“三段论”，其推理是这样的：对于可导函数，若，则是函数的极值点,因为函数满足，所以是函数的极值点”，结论以上推理　　

A. 大前提错误B. 小前提错误C. 推理形式错误D. 没有错误

【题目】正四棱锥的底面正方形边长是3，是在底面上的射影，，是上的一点，过且与、都平行的截面为五边形．

（1）在图中作出截面，并写出作图过程；

（2）求该截面面积的最大值．

【题目】为响应国家提出的“大众创业，万众创新”的号召,小李同学大学毕业后,决定利用所学专业进行自主创业。经过市场调查,生产某小型电子产品需投入年固定成本为5万元，每年生产万件，需另投入流动成本为万元，且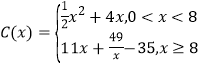，每件产品售价为10元。经市场分析,生产的产品当年能全部售完。

(1)写出年利润(万元)关于年产量(万件)的函数解析式；

(注:年利润=年销售收入-固定成本-流动成本)

(2)年产量为多少万件时，小李在这一产品的生产中所获利润最大?最大利润是多少?

【题目】如图，长方体ABCD﹣A1B1C1D1中，DA＝DC＝2，，E是C1D1的中点，F是CE的中点．

（1）求证：EA∥平面BDF；

（2）求证：平面BDF⊥平面BCE；

（3）求二面角D﹣EB﹣C的正切值．

【题目】已知函数，对任意的，满足，其中为常数．

（Ⅰ）若,求在处的切线方程；

（Ⅱ）已知,求证；

（Ⅲ）当存在三个不同的零点时，求的取值范围．

（1）试估算该市“足球迷”的人数，并指出其中“铁杆足球迷”约为多少人；

（2）该市要举办一场足球比赛，已知该市的足球场可容纳10万名观众．根据调查，如果票价定为100元/张，则非“足球迷”均不会到现场观看，而“足球迷”均愿意前往现场观看．如果票价提高元/张，则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少，“铁杆足球迷”愿意前往观看的人数会减少．问票价至少定为多少元/张时，才能使前往现场观看足球比赛的人数不超过10万人？

【题目】已知函数为奇函数.

（1）求实数的值；

（2）用定义法讨论并证明函数的单调性.

【题目】某科研单位在研发钛合金产品的过程中发现了一种新合金材料，由大数据测得该产品的性能指标值（值越大产品的性能越好）与这种新合金材料的含量（单位：克）的关系：当时，是的二次函数；当时，.测得部分数据如表所示.

（1）求关于的函数关系式；

（2）求该新合金材料的含量为何值时产品的性能达到最佳.