
科目: 来源: 题型:
【题目】已知函数f(x)g(x)分别是定义在R上的偶函数和奇函数,且f(x)+g(x)=23x.
(1)证明:f(x)-g(x)=23-x,并求函数f(x),g(x)的解析式;
(2)解关于x不等式:g(x2+2x)+g(x-4)>0;
(3)若对任意x∈R,不等式f(2x)≥mf(x)-4恒成立,求实数m的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 与双曲线
与双曲线![]() 有公共焦点
有公共焦点![]() ,点
,点![]() 是曲线
是曲线![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.
(Ⅰ)求双曲线![]() 的方程;
的方程;
(Ⅱ)以双曲线![]() 的另一焦点
的另一焦点![]() 为圆心的圆
为圆心的圆![]() 与直线
与直线![]() 相切,圆
相切,圆![]() .过点
.过点![]() 作互相垂直且分别与圆
作互相垂直且分别与圆![]() 、圆
、圆![]() 相交的直线
相交的直线![]() 和
和![]() ,设
,设![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,
,![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,问:
,问:![]() 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点 在椭圆上.
在椭圆上.
(![]() )求椭圆
)求椭圆![]() 的方程.
的方程.
(![]() )设动直线
)设动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,判断是否存在以原点
有且仅有一个公共点,判断是否存在以原点![]() 为圆心的圆,满足此圆与
为圆心的圆,满足此圆与![]() 相交于两点
相交于两点![]() ,
, ![]() (两点均不在坐标轴上),且使得直线
(两点均不在坐标轴上),且使得直线![]() 、
、![]() 的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】学校书店新进了一套精品古典四大名著:《红楼梦》、《三国演义》、《西游记》、《水浒传》共四本书,每本名著数量足够多,今有五名同学去书店买书,由于价格较高,五名同学打算每人只选择一本购买.
(1)求“每本书都有同学买到”的概率;
(2)求“对于每个同学,均存在另一个同学与其购买的书相同”的概率;
(3)记X为五位同学购买相同书的个数的最大值,求X的分布列和数学期望E(X).
查看答案和解析>>
科目: 来源: 题型:
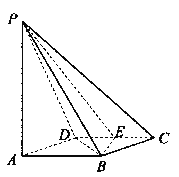
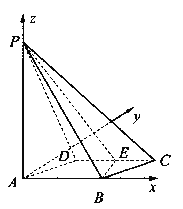
【题目】如图所示,四棱锥![]() 的底面
的底面![]() 是边长为1的菱形,
是边长为1的菱形,![]() ,
,
E是CD的中点,PA![]() 底面ABCD,
底面ABCD,![]() .
.
(I)证明:平面PBE![]() 平面PAB;
平面PAB;
(II)求二面角A—BE—P和的大小.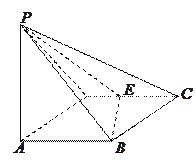
查看答案和解析>>
科目: 来源: 题型:
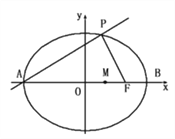
【题目】如图,A、B分别是椭圆![]() 的左、右端点,F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF.
的左、右端点,F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF.
(1)点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于MB,求椭圆上的点到点M的距离d的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某连锁餐厅新店开业打算举办一次食品交易会,招待新老顾客试吃项目经理通过查阅最近5次食品交易会参会人数x(万人)与餐厅所用原材料数量y(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数(万人) | 13 | 9 | 8 | 10 | 12 |
原材料(袋) | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出y关于x的线性回归方程![]()
(2)已知购买原材料的费用C(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有13万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料才能获得最大利润,最大利润是多少?(注:利润L=销售收入-原材料费用)
,投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有13万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料才能获得最大利润,最大利润是多少?(注:利润L=销售收入-原材料费用)
参考公式: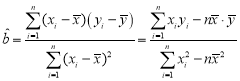 ,
,![]()
参考数据:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com