
科目: 来源: 题型:
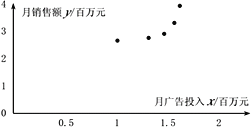
【题目】长沙某公司对其主推产品在过去5个月的月广告投入xi(百万元)和相应的销售额yi(百万元)进行了统计,其中i=1,2,3,4,5,对所得数据进行整理,绘制散点图并计算出一些统计量如下:
|
|
|
|
|
|
|
68 | 10.3 | 15.8 | -192.12 | 1.602 | 0.46 | 3.56 |
其中![]() ,i=1,2,3,4,5.
,i=1,2,3,4,5.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为月销售额关于月广告投入xi的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为月销售额关于月广告投入xi的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及题中所给数据,建立y关于x的回归方程,并据此估计月广告投入200万元时的月销售额.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: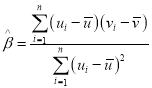 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,半径为![]() 的水轮绕着圆心
的水轮绕着圆心![]() 逆时针做匀速圆周运动,每分钟转动
逆时针做匀速圆周运动,每分钟转动![]() 圈,水轮圆心
圈,水轮圆心![]() 距离水面
距离水面![]() ,如果当水轮上点
,如果当水轮上点![]() 从离开水面的时刻(
从离开水面的时刻(![]() )开始计算时间.
)开始计算时间.
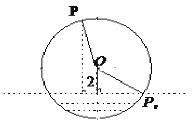
(1)试建立适当的平面直角坐标系,求点![]() 距离水面的高度
距离水面的高度![]() (
(![]() )与时间
)与时间![]() (
(![]() )满足的函数关系;
)满足的函数关系;
(2)求点![]() 第一次到达最高点需要的时间.
第一次到达最高点需要的时间.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}中,a1=1且an﹣an﹣1=3×(![]() )n﹣2(n≥2,n∈N*).
)n﹣2(n≥2,n∈N*).
(1)求数列{an}的通项公式:
(2)若对任意的n∈N*,不等式1≤man≤5恒成立,求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业有2个分厂生产某种零件,为了研究两个分厂生产零件的质量是否有差异,随机从2个分厂生产的零件中各抽取了500件,具体数据如下表所示:
甲厂 | 乙厂 | 总计 | |
优质品 | 360 | 320 | 680 |
非优质品 | 140 | 180 | 320 |
总计 | 500 | 500 | 1000 |
根据表中数据得![]() 的观测值
的观测值![]() ,从而断定两个分厂生产零件的质量有差异,那么这种判断出错的最大可能性为( )
,从而断定两个分厂生产零件的质量有差异,那么这种判断出错的最大可能性为( )
附表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A.0.1B.0.01C.0.05D.0.001
查看答案和解析>>
科目: 来源: 题型:
【题目】已知两圆C1:x2+y2-2x-6y-1=0和C2:x2+y2-10x-12y+45=0.
(1)求证:圆C1和圆C2相交;
(2)求圆C1和圆C2的公共弦所在直线的方程和公共弦长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C:![]() 上顶点为A,右顶点为B,离心率
上顶点为A,右顶点为B,离心率![]() ,O为坐标原点,原点到直线AB的距离为
,O为坐标原点,原点到直线AB的距离为![]() .
.
(1)求椭圆C的标准方程;
(2)直线![]() 与椭圆C相交于E、F两不同点,若椭圆C上一点P满足
与椭圆C相交于E、F两不同点,若椭圆C上一点P满足![]() .求△EPF面积的最大值及此时的
.求△EPF面积的最大值及此时的![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com