
科目: 来源: 题型:
【题目】2018年为我国改革开放40周年,某事业单位共有职工600人,其年龄与人数分布表如下:
年龄段 |
|
|
|
|
人数(单位:人) | 180 | 180 | 160 | 80 |
约定:此单位45岁~59岁为中年人,其余为青年人,现按照分层抽样抽取30人作为全市庆祝晚会的观众.
(1)抽出的青年观众与中年观众分别为多少人?
(2)若所抽取出的青年观众与中年观众中分别有12人和5人不热衷关心民生大事,其余人热衷关心民生大事.完成下列![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为年龄层与热衷关心民生大事有关?
的把握认为年龄层与热衷关心民生大事有关?
热衷关心民生大事 | 不热衷关心民生大事 | 总计 | |
青年 | 12 | ||
中年 | 5 | ||
总计 | 30 |
(3)若从热衷关心民生大事的青年观众(其中1人擅长歌舞,3人擅长乐器)中,随机抽取2人上表演节目,则抽出的2人能胜任才艺表演的概率是多少?
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
 .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线C的极坐标方程为ρ=4cosθ,以极点为原点,极轴为x轴正半轴建立平面直角坐标系,设直线l的参数方程为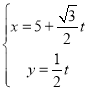 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程与直线l的普通方程;
(2)设曲线C与直线l相交于P,Q两点,以PQ为一条边作曲线C的内接矩形,求该矩形的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】研究变量![]() ,
,![]() 得到一组样本数据,进行回归分析,有以下结论
得到一组样本数据,进行回归分析,有以下结论
①残差平方和越小的模型,拟合的效果越好;
②用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小说明拟合效果越好;
越小说明拟合效果越好;
③在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,预报变量
每增加1个单位时,预报变量![]() 平均增加0.2个单位
平均增加0.2个单位
④若变量![]() 和
和![]() 之间的相关系数为
之间的相关系数为![]() ,则变量
,则变量![]() 和
和![]() 之间的负相关很强,以上正确说法的个数是( )
之间的负相关很强,以上正确说法的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】记无穷数列![]() 的前n项中最大值为
的前n项中最大值为![]() ,最小值为
,最小值为![]() ,令
,令![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() .
.
(1)若数列![]() 是首项为2,公比为2的等比数列,求
是首项为2,公比为2的等比数列,求![]() ;
;
(2)若数列![]() 是等差数列,试问数列
是等差数列,试问数列![]() 是否也一定是等差数列?若是,请证明;若不是,请举例说明;
是否也一定是等差数列?若是,请证明;若不是,请举例说明;
(3)若![]() ,求
,求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=(3-x)ex,g(x)=x+a(a∈R)(e是自然对数的底数,e≈2.718…).
(1)求函数f(x)的极值;
(2)若函数y=f(x)g(x)在区间[1,2]上单调递增,求实数a的取值范围;
(3)若函数h(x)=![]() 在区间(0,+∞)上既存在极大值又存在极小值,并且函数h(x)的极大值小于整数b,求b的最小值.
在区间(0,+∞)上既存在极大值又存在极小值,并且函数h(x)的极大值小于整数b,求b的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地最近十年粮食需求量逐年上升,下表是部分统计数据:
年份 | 2006 | 2008 | 2010 | 2012 | 2014 |
需求量/万吨 | 236 | 246 | 257 | 276 | 286 |
(1)利用所给数据求年需求量![]() 与年份
与年份![]() 之间的线性回归方程
之间的线性回归方程![]() ;
;
(2)利用(1)中所求出的线性回归方程预测该地2018年的粮食需求量.
参考公式: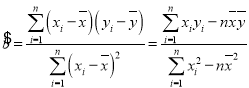 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,椭圆M:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,左右顶点分別为A,B,线段AB的长为4.P在椭圆M上且位于第一象限,过点A,B分别作l1⊥PA,l2⊥PB,直线l1,l2交于点C.
,左右顶点分別为A,B,线段AB的长为4.P在椭圆M上且位于第一象限,过点A,B分别作l1⊥PA,l2⊥PB,直线l1,l2交于点C.

(1)若点C的横坐标为﹣1,求P点的坐标;
(2)直线l1与椭圆M的另一交点为Q,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
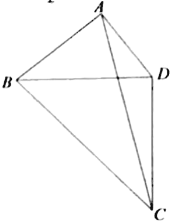
【题目】为了美化环境,某公园欲将一块空地规划建成休闲草坪,休闲草坪的形状为如图所示的四边形ABCD.其中AB=3百米,AD=![]() 百米,且△BCD是以D为直角顶点的等腰直角三角形.拟修建两条小路AC,BD(路的宽度忽略不计),设∠BAD=
百米,且△BCD是以D为直角顶点的等腰直角三角形.拟修建两条小路AC,BD(路的宽度忽略不计),设∠BAD=![]() ,
,![]() (
(![]() ,
,![]() ).
).
(1)当cos![]() =
=![]() 时,求小路AC的长度;
时,求小路AC的长度;
(2)当草坪ABCD的面积最大时,求此时小路BD的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高二年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高二年级抽取了45名学生的测评结果,并作出频数统计表如下:
表1:男生
等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 |
| 5 |
表2:女生
等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 | 3 |
|
(1)由表中统计数据填写下边![]() 列联表:
列联表:
男生 | 女生 | 总计 | |||||
优秀 | |||||||
非优秀 | 总计 |
(2)试采用独立性检验进行分析,能否在犯错误的概率不超过0.1的前提下认为“测评结果优秀与性别有关”.
参考数据与公式: ,其中
,其中![]() .
.
临界值表:
| 0.1 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com