
科目: 来源: 题型:
【题目】我国是世界第一产粮大国,我国粮食产量很高,整体很安全按照14亿人口计算,中国人均粮食产量约为950斤﹣比全球人均粮食产量高了约250斤.如图是中国国家统计局网站中2010﹣2019年,我国粮食产量(千万吨)与年末总人口(千万人)的条形图,根据如图可知在2010﹣2019年中( )
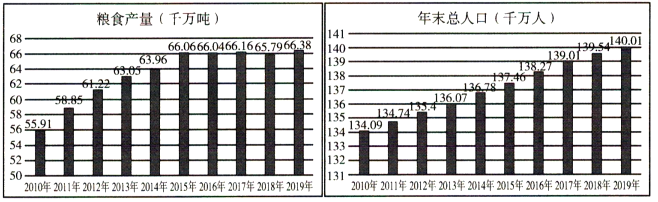
A.我国粮食年产量与年末总人口均逐年递增
B.2011年我国粮食年产量的年增长率最大
C.2015年﹣2019年我国粮食年产量相对稳定
D.2015年我国人均粮食年产量达到了最高峰
查看答案和解析>>
科目: 来源: 题型:
【题目】在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .现以极点
.现以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的非负半轴建立平面直角坐标系,直线
轴的非负半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为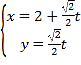 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标系方程和直线
的直角坐标系方程和直线![]() 的普通方程;
的普通方程;
(2)点![]() 在曲线
在曲线![]() 上,且到直线
上,且到直线![]() 的距离为
的距离为![]() ,求符合条件的
,求符合条件的![]() 点的直角坐标.
点的直角坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知球![]() 是正三棱锥(底面为正三角形,顶点在底面的射影为底面中心)
是正三棱锥(底面为正三角形,顶点在底面的射影为底面中心)![]() 的外接球,
的外接球,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() ,过点
,过点![]() 作球
作球![]() 的截面,则所得截面圆面积的取值范围是( )
的截面,则所得截面圆面积的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级:0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;>300为严重污染.一环保人士记录了某地2020年某月10天的AQI的茎叶图如图所示.
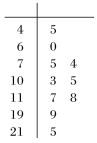
(1)利用该样本估计该地本月空气质量优良(AQI≤100)的天数;(按这个月总共有30天计算)
(2)若从样本中的空气质量不佳(AQI>100)的这些天中,随机地抽取两天深入分析各种污染指标,求该两天的空气质量等级恰好不同的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() 与直线
与直线![]() :
:![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)若![]() 的面积为
的面积为![]() ,求
,求![]() ;
;
(2)![]() 轴上是否存在点
轴上是否存在点![]() ,使得当
,使得当![]() 变动时,总有
变动时,总有![]() ?若存在,求以线段
?若存在,求以线段![]() 为直径的圆的方程;若不存在,请说明理由.
为直径的圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】每年春晚都是万众瞩目的时刻,这些节目体现的文化内涵、历史背景等反映了社会的进步.国家的富强,人民生活水平的提高等.某学校高三年级主任开学初为了解学生在看春晚后对节目体现的文化内涵、历史背景等是否会在今年的高考题中体现进行过思考,特地随机抽取100名高三学生(其中文科学生50,理科学生50名),进行了调查.统计数据如表所示(不完整):
“思考过” | “没有思考过” | 总计 | |
文科学生 | 40 | 10 | |
理科学生 | 30 | ||
总计 | 100 |
(1)补充完整所给表格,并根据表格数据计算是否有![]() 的把握认为看春晚后会思考节目体现的文化内涵、历史背景等与文理科学生有关;
的把握认为看春晚后会思考节目体现的文化内涵、历史背景等与文理科学生有关;
(2)①现从上表的”思考过”的文理科学生中按分层抽样选出7人.再从这7人中随机抽取4人,记这4人中“文科学生”的人数为![]() ,试求
,试求![]() 的分布列与数学期望;
的分布列与数学期望;
②现设计一份试卷(题目知识点来自春晚相关知识整合与变化),假设“思考过”的学生及格率为![]() ,“没有思考过”的学生的及格率为
,“没有思考过”的学生的及格率为![]() .现从“思考过”与“没有思考过”的学生中分别随机抽取一名学生进行测试,求两人至少有一个及格的概率.
.现从“思考过”与“没有思考过”的学生中分别随机抽取一名学生进行测试,求两人至少有一个及格的概率.
附参考公式: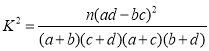 ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】某公交公司为了方便市民出行、科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为研究车辆发车间隔时间![]() (分钟)与乘客等候人数
(分钟)与乘客等候人数![]() (人)之间的关系,经过调查得到如下数据:
(人)之间的关系,经过调查得到如下数据:
间隔时间 |
|
|
|
|
|
|
等候人数 |
|
|
|
|
|
|
调查小组先从这![]() 组数据中选取
组数据中选取![]() 组数据求线性回归方程,再用剩下的
组数据求线性回归方程,再用剩下的![]() 组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数
组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数
与实际等候人数![]() 的差,若差值的绝对值不超过
的差,若差值的绝对值不超过![]() ,则称所求线性回归方程是“恰当回归方程”.
,则称所求线性回归方程是“恰当回归方程”.
(1)从这![]() 组数据中随机选取
组数据中随机选取![]() 组数据后,求剩下的
组数据后,求剩下的![]() 组数据的间隔时间之差大于
组数据的间隔时间之差大于![]() 的概率;
的概率;
(2)若选取的是后面![]() 组数据,求
组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并判断此方程是否是“恰当回归方程”;
,并判断此方程是否是“恰当回归方程”;
(3)在(2)的条件下,为了使等候的乘客不超过![]() 人,则间隔时间最多可以设置为多少分钟?(精确到整数)
人,则间隔时间最多可以设置为多少分钟?(精确到整数)
参考公式: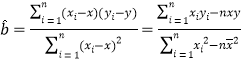 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com